Question

A block tied between two identical springs is in equilibrium. If the upper spring is cut, then the acceleration of the block just after the cut is $5 \mathrm{ms}^{-2}$. Now if instead of upper string lower spring is cut, then the acceleration of the block just after the cut will be (Take $g=10m/{{s}^{2}}$)

A $1.25 \mathrm{m} / \mathrm{s}^{2}$
B $5 \mathrm{m} / \mathrm{s}^{2}$
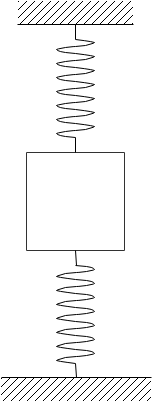
C $10 \mathrm{m} / \mathrm{s}^{2}$
D $2.5 \mathrm{m} / \mathrm{s}^{2}$

Answer 1

We know that mechanics is the area of physics concerned with the motions of macroscopic objects. Forces applied to objects result in displacements, or changes of an object's position relative to its environment. Keeping this in mind, we can solve the given question.

Complete step by step answer
From the given question,
Let x be the displacement of each spring in equilibrium before any of the spring is cut. For such a situation, the upper spring stretches to exert a force on the body in the upward direction. Similarly, the lower spring compresses to exert a force on the body in the upward direction. Thus $\mathrm{kx}+\mathrm{kx}=\mathrm{mg}$
$\Rightarrow x=\dfrac{mg}{2k}$
Now when the upper spring is cut, the forces acting on the body are mg downwards and kx upwards. Thus, the acceleration of body $=\dfrac{\mathrm{mg}-\mathrm{kx}}{\mathrm{m}}=\dfrac{\mathrm{g}}{2}=5 \mathrm{m} / \mathrm{s}^{2}$ downwards
Now when the lower spring is cut, the forces acting are mg downwards and kx upwards again. Thus, the acceleration is $5 \mathrm{m} / \mathrm{s}^{2}$ downwards.

Therefore, the correct answer is Option B.

Note: We must effectively be able to draw free body diagrams. Free-body diagrams are diagrams used to show the relative magnitude and direction of all forces acting upon an object in a given situation. A free-body diagram is a special example of the vector diagrams.