Question
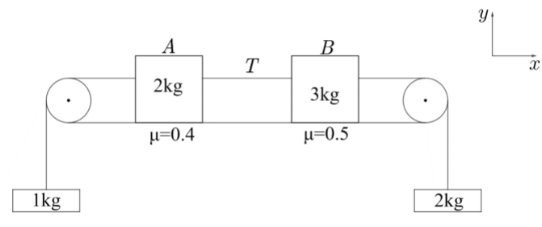
Question: A block system is shown in figure. Frictional force on \(2kg\) is \({{f}_{1}}\) and on \(3kg\) is \(...
A block system is shown in figure. Frictional force on 2kg is f1 and on 3kg is f2 and T is tension in the string connecting block A and B. Which of the following is correct?
A. f1=8i^,f2=−15i^,T=2N
B. f1=5i^,f2=−15i^,T=5N
C. f1=−8i^,f2=−15i^,T=2N
D. f1=−5i^,f2=−15i^,T=5N
Solution
Draw the free body diagram of all the blocks and balance the forces. A free body diagram is a sketch of an object of interest with the entire surrounding object stripped away and all the forces acting on the body are shown, it helps to visualize all the forces acting on a single object.
Complete step by step answer:
The blocks of 1kg and 2kg will experience gravitational force in downward direction due to their weight. Gravitation force on 2kg block W=mg, take g=10 ms−2
W=2×10 ⇒W=20N
Gravitation force on 1kg block W=mg, take g=10 ms−2
W=1×10 ⇒W=10N
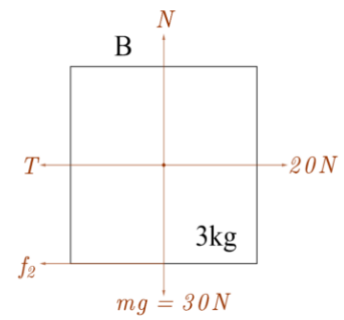
Free body diagram of Block B
Normal force (N) is a contact force that is felt when a surface pushes against an object that is placed on that surface and is perpendicular to the surface that an object contacts.
Since the body is not going anywhere in a vertical direction, upward and downward force will be equal in magnitude.
N=mg, here mass of the block is 3kg.
N=3×10=30N
Normal force on block B is 30N. Frictional force is the resistance force against motion of one object moving relative to another. It is in the opposite direction to motion of the object.
f2max=μN=0.5×30=15N (μ=0.5 for block B and N represents normal reaction)
Let the block B start moving in x direction with acceleration a.
ma=20−T−f2
3a=20−T−f2.........(1)
Since the block is at rest a=0, the equation will become;
20=T+f2............(2)

Since the body is not going anywhere in a vertical direction, upward and downward force will be equal in magnitude.
N=mg, here mass of the block is 2kg
N=2×10=20N
f1max=μN=0.4×20=8N (μ=0.4 for block A and N represents normal reaction)
Let the block B start moving in x direction with acceleration a.
2a=T−10−f1........(3)
Since the block is at rest a=0, the equation will become;
T−f1=10 .............(4)
Add (2)and(4)
f1+f2=10.......(5)
Using (2),(4)and(5)
We will get f1=−5i^,f2=−15i^,T=5N
Therefore option D is the correct answer.
Note: Friction always slows a motion and amount of friction depends on the material from which those two surfaces are made. To stop the motion block A will provide 5N friction and block B will give 15N friction.
