Question

A block slides down on an inclined plane of slope angle $\theta$ with constant velocity. It is then projected up on the same plane with initial velocity ${V_0}$. How far up the incline will it move before coming to rest
A. $\dfrac{{V_0^2}}{{g\sin \theta }}$
B. $\dfrac{{V_0^2}}{{2g\sin \theta }}$
C. $\dfrac{{V_0^2}}{{4g\sin \theta }}$
D. $\dfrac{{V_0^2}}{{8g\sin \theta }}$

Answer 1

Use the expression for Newton’s second law of motion. Draw a free body diagram of the block when it is sliding down and determine the value for coefficient of friction between the block and inclined plane. Then draw the free body diagram of the block while moving up on the plane and determine acceleration of the block. Using a second kinematic equation determines the displacement of the block before coming to rest.

Formula used:
The expression for Newton’s second law of motion is
${F_{net}} = ma$ …… (1)
Here, ${F_{net}}$ is the net force on an object, $m$ is mass of the object and $g$ is acceleration of the object.
The frictional force ${F_f}$ on an object is
${F_f} = \mu N$ …… (2)
Here, $\mu$ is the coefficient of friction and $N$ is the normal force on the object.
The kinematic equation relating final velocity $v$, initial velocity $u$, acceleration $a$ and displacement $s$ of an object is
${v^2} = {u^2} + 2as$ …… (3)

Complete step by step solution:
We have given that the block is sliding down from an inclined plane having angle of inclination $\theta$ with the horizontal.

Let $m$ be the mass of the block.

Draw the free body diagram of the block when it is sliding down the inclined plane.

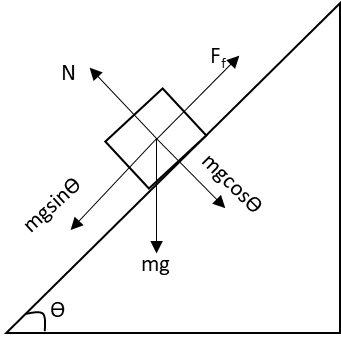
In the above free body diagram, $mg$ is the weight of the block acting in the downward direction, $N$ is the normal force exerted by the inclined plane on the block and ${F_f}$ is the frictional force acting on the block when it is sliding down. The components of weight of the block are shown in the diagram.

Since the block is sliding down with a uniform velocity, the acceleration of the block is zero.

Let us determine the value of coefficient of friction between the block and inclined plane.

Apply Newton’s second law of motion to the block in horizontal direction.
${F_f} = mg\sin \theta$

Apply Newton’s second law of motion to the block in vertical direction.
$N = mg\cos \theta$

Rearrange equation (2) for coefficient of friction between the block and inclined plane.
$\mu = \dfrac{{{F_f}}}{N}$

Substitute $mg\sin \theta$ for ${F_f}$ and $mg\cos \theta$ for $N$ in the above equation.
$\mu = \dfrac{{mg\sin \theta }}{{mg\cos \theta }}$
$\Rightarrow \mu = \tan \theta$

While moving upward, the initial velocity of the block is ${V_0}$ which is not uniform. So, we have to determine the acceleration of the block while moving upward.

Draw the free body diagram of the block when it is moving upward.

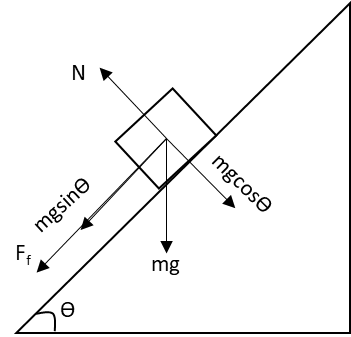
The free body diagram of the block while moving upwards is the same as before. Only the direction of the frictional force is reversed while moving upward.

Apply Newton’s second law of motion to the block in the horizontal direction.
$- {F_f} - mg\sin \theta = ma$
$- {F_f} - mg\sin \theta = ma$

Substitute for ${F_f}$ in the above equation and solve it for $a$.
$\mu N + mg\sin \theta = ma$

Substitute $\tan \theta$ for $\mu$ and $mg\cos \theta$ for $N$ in the above equation.
$- \left( {\tan \theta } \right)\left( {mg\cos \theta } \right) - mg\sin \theta = ma$
$\Rightarrow a = - 2g\sin \theta$

Let us now determine the displacement of the block before it comes to rest.

The final velocity of the block is zero, as it comes to rest.

Rewrite equation (3) for the block while moving upward.
$0 = V_0^2 + 2as$
$\Rightarrow s = \dfrac{{ - V_0^2}}{{2a}}$

Substitute $a$ for $- 2g\sin \theta$ in the above equation.
$\Rightarrow s = \dfrac{{ - V_0^2}}{{2\left( { - 2g\sin \theta } \right)}}$
$\Rightarrow s = \dfrac{{V_0^2}}{{4g\sin }}$

Therefore, the distance travelled by the block before coming to rest is $\dfrac{{V_0^2}}{{4g\sin }}$.

So, the correct answer is “Option C”.

Note:
The students may think that the acceleration of the block while moving up is negative. The block is moving upwards against the direction of frictional force and horizontal component of its weight. These forces are opposing the motion of the block. Thus, the block undergoes retardation (negative acceleration) and then stops.