Question

A block slides down an inclined plane of slope of angle $\theta$ with a constant velocity $v$ . It is then projected up the plane with an initial velocity $u$ . What is the distance up to which it will rise before coming to rest?

Answer 1

We are given here with the angle of inclination of the slope and are being told that the block is being projected upwards with initial velocity $u$ after it slides down. We are asked to find the distance up to which the block will rise before coming to rest. Thus, we will use the concept of friction on a slope and then we will use the equations of motion to find the rise of the block.

Formulae used:
${v^2} - {u^2} = 2as$
Where, $v$ is the final velocity of the object, $u$ is the initial velocity of the object, $a$ is the acceleration on the object and $s$ is the displacement of the object.

Complete step by step solution:
Here, We try to draw a free body diagram for the situation of the block sliding down and reaching the bottom of the slope.

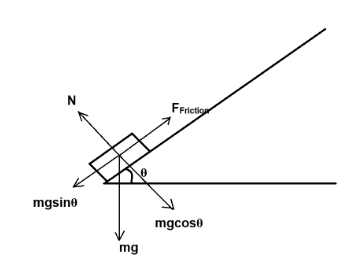
Now,
As the block is sliding down with a constant velocity, there will be no acceleration of the block.
Thus, we get
${F_{Friction}} = mg\sin \theta$
But,
We know that,
${F_{Friction}} = {\mu _s}N$
And according to the diagram,
$N = mg\cos \theta$
Thus, we get
${\mu _s}mg\cos \theta = mg\sin \theta$
Thus, we get
${\mu _S} = \tan \theta \cdot \cdot \cdot \cdot \left( 1 \right)$
Now,
As we launch the block upwards, there will be a force in the opposite direction of value ${\mu _S}mg\cos \theta$ .
Thus,
The net acceleration on the block will be given by,
$a = g\sin \theta + {\mu _S}g\cos \theta$
Substituting equation $\left( 1 \right)$ in the above equation, we get
$a = 2g\sin \theta$
Now,
Applying the equation of motion,
${v^2} - {u^2} = 2as$
Here, the acceleration will be negative as the block is launched upwards and the acceleration is downwards.
Also,
The final velocity of the block when it reaches the maximum height is $0$ .
Thus, the equation turns out to be,
$0 - {u^2} = 2( - 2g\sin \theta )h$
After further evaluation, we get
${u^2} = 4gh\sin \theta$
Thus,
The final equation turns out to be
$h = \dfrac{{{u^2}}}{{4g\sin \theta }}$ .

Note:
We have taken the acceleration as the cosine function of the angle of inclination but it is up to us. If we want, we can have the sine function of the angle by just adding a value of $\dfrac{\pi }{2}$ to the angle of inclination. But though the final answer will remain the same.