Question

A block slides down a rough inclined plane of inclination ${45^ \circ }$. If the coefficient of kinetic friction is $0.5$, find the acceleration of the sliding block. (Take $g = 10m{s^{ - 2}}$ )

Answer 1

This problem can be solved by drawing the forces acting on the body such as the normal force, the frictional force, and the force acting on the body due to gravity. In addition to this drawing the components of force, mg will aid in solving this problem. After this equate the force in terms of mass multiplied by acceleration to the different forces acting on the body.
Formula used:
Force $F = \;ma$ , $m$ is the mass of the block and $a$ is acceleration
$\cos {45^ \circ } = \sin {45^ \circ } = \dfrac{1}{{\sqrt 2 }}$

Complete step-by-step solution:

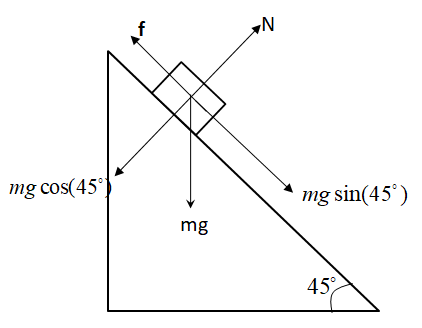
The given values are the angle of inclination ${45^ \circ }$ and coefficient of friction $\mu = 0.5$ .
We need to find the acceleration with which the block is sliding down the inclined plane.
There is a normal force$\left( N \right)$ , acting perpendicular to the block, a downward force $mg$ , and a frictional force $\left( f \right)$ that is opposing the movement of the block. The forces mg$mg\sin 45^\circ$ and $mg\cos 45^\circ$ are the components of force $mg$.
Normal force $\left( N \right)$ and $mg\cos 45^\circ$ are equal forces in opposite directions.
Hence, $N = mg\cos 45^\circ$
When we write the block sliding on the inclined plane in terms of force we get,
$F = mg\sin {45^ \circ } - f$ , this is because the sliding force $mg\sin {45^ \circ }$ is greater than the frictional force
Substitute, a force equal to mass multiplied by acceleration. That is in mathematical terms F$=$ma in the above equation (F-force, m-mass, a-acceleration)
We get, $ma = mg\sin {45^ \circ } - f$……… (1)
The frictional force $= \mu N = \mu \times mg\cos {45^ \circ }$……….. (2)
Substitute equation (2) in equation (1)
Therefore we get, ma$ma = mg\sin {45^ \circ } - \mu mg\cos {45^ \circ }$
Cancelling the common term in the equation
We get, $a = g\sin {45^ \circ } - \mu g\cos {45^ \circ }$
Substituting the value of $\sin {45^ \circ }$ and $\cos {45^ \circ }$in the above equation,
We get, $a = g\dfrac{1}{{\sqrt 2 }} - \mu g\dfrac{1}{{\sqrt 2 }}$
Now substitute the given values $g = 10$ and $\mu = 0.5$
We get acceleration,
$a = \dfrac{{10}}{{\sqrt 2 }} - \dfrac{5}{{\sqrt 2 }} = \dfrac{5}{{\sqrt 2 }}$
$= 5 \times 0.707 = 3.535m{s^{ - 2}}$
The acceleration of the block sliding across the inclined plane is $3.535m{s^{ - 2}}$

Note: While solving this question care must be taken to mention the equation of force. That is, since the block is sliding down, the equation must be written as ,$F = mg\sin {45^ \circ } - f$ and not $F = f - mg\sin {45^ \circ }$. There is a frictional force hindering the movement of the block but since the block is sliding down the force mg$\sin {45^ \circ }$is greater than the frictional force.