Solveeit Logo
Login

Question

Question: A block slide down an inclined plane (angle of inclination \({{60}^{0}}\) ) with an acceleration g/2...

A block slide down an inclined plane (angle of inclination 600{{60}^{0}} ) with an acceleration g/2. Find the coefficient of kinetic friction.

Explanation

Solution

Hint : Here we need to find the frictional force on the box and the acceleration of the box due to its weight. Draw a free body diagram. Obtain the components of the weight of the box. By balancing them we can find the acceleration of the box. Now equating this with the given acceleration in terms of the force, we can find the coefficient of friction.

Complete step by step solution :
The block is sliding down the inclined plane.
Let the mass of the block is m.
The weight of the block will be mg, where g is the acceleration due to gravity.
Draw the free body diagram of the system.

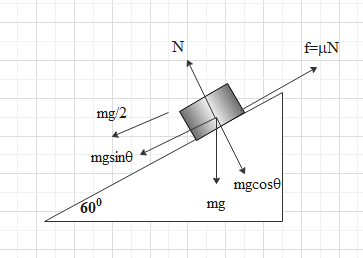
The normal force on the block will be,
N=mgcos⁡θN=mg\cos \theta
Where, N is the normal force, m is the mass of the block, g is the acceleration due to gravity and θ\theta is the angle of inclination of the inclined plane.
Now, let the coefficient of kinetic friction on the block is μ\mu .
So, the frictional force will be,
f=μN f=μmgcos⁡θ \begin{aligned} & f=\mu N \\\ & f=\mu mg\cos \theta \\\ \end{aligned}
Again, the acceleration of the body down the inclined plane is g/2g/2 . so, we can write that,
mg2=mgsin⁡θ−fm\dfrac{g}{2}=mg\sin \theta -f
Also, the angle of inclination of the inclined plane is 600{{60}^{0}}
Putting this value on the above equation, we get that,
mg2=mgsin⁡600−μmgcos⁡600 12=sin⁡600−μcos⁡600 12=32−μ×12 1=3−μ μ=3−1 μ=1.73−1 μ=0.73 \begin{aligned} & m\dfrac{g}{2}=mg\sin {{60}^{0}}-\mu mg\cos {{60}^{0}} \\\ & \dfrac{1}{2}=\sin {{60}^{0}}-\mu \cos {{60}^{0}} \\\ & \dfrac{1}{2}=\dfrac{\sqrt{3}}{2}-\mu \times \dfrac{1}{2} \\\ & 1=\sqrt{3}-\mu \\\ & \mu =\sqrt{3}-1 \\\ & \mu =1.73-1 \\\ & \mu =0.73 \\\ \end{aligned}
So, the coefficient of kinetic friction will be, 0.73

Note : We have two types of friction. The static friction opposes the motion of a block of mass. Kinetic friction can be defined as the force which opposes the motion of a block of mass in motion. The coefficient of static friction and coefficient of kinetic friction are both different. Static frictional force can be found by equating the force applied on the box even after which the box is at rest.