Question

A block rests on a rough inclined plane as shown in fig. A horizontal force $F$ is applied to it.
(a) Find the force of normal reaction.
(b) Can the force of friction be zero, if yes when?
(c) Assuming that friction is not zero, find its magnitude and direction of its limiting value.

Answer 1

Find the equation of motion of the block at equilibrium. Newton’s second law of motion states that the force is equal to the mass times the acceleration of the body. The force acting on the body here is the applied force, the gravity and the frictional force.

Formula used:
The equation of motion of a body at equilibrium is given by,
${F_{net}} = 0$
Where ${F_{net}}$ is the net applied force.
The limiting frictional force acting on a body at rest is given by,
${F_f} \leqslant \mu N$
where $\mu$ is the coefficient of static friction and is $N$ the normal force of the body due to the surface.

Complete step by step answer:
We have given here a block which is resting on the slanted surface and a horizontal force is applied to it. Now, we know that the block will be at rest if the net force acting on the block is zero, ${F_{net}} = 0$ Where ${F_{net}}$ is the net applied force. Let, the mass of the block is m and the coefficient of friction of the block is $\mu$. Now, we can draw the force diagram of the block as follows.

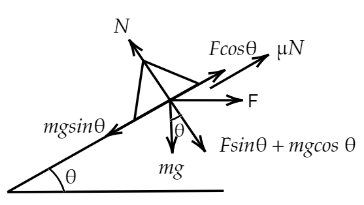
From the force diagram we can see that the vertical component of forces is the component of the weight of the body and the applied force. So, it will be equal to the normal force due to the surface. Hence, for vertical component we can write,
$N = F\sin \theta + mg\cos \theta {\text{ }}$….(1)

(a) So, the normal force by the surface is equal to $F\sin \theta + mg\cos \theta {\text{ }}$.
Now, for horizontal component of forces we can write the equation of motion as,
$mg\sin \theta - F\cos \theta - \mu N = 0$

(b) Now, we know that the friction force can only be zero for two cases:
-If the normal force is zero, and
-If the coefficient of friction is zero.
If we apply the first condition we have, $F\sin \theta = - mg\cos \theta {\text{ }}$ meaning that the component of gravity must be equal and opposite to the sine component of the applied force. For the second condition if the surface is smooth enough and if it can be made ideally to zero then the frictional force will be zero which is not possible in real life.For both of the cases the for horizontal direction we will have $mg\sin \theta = F\cos \theta$.

(c) Now, if the frictional force is not zero from equation (1) and (2) we can write,
$mg\sin \theta - F\cos \theta - \mu N = 0$
${F_f} = \mu N = mg\sin \theta - F\cos \theta$
So, the minimum value of the frictional force must be equal to $mg\sin \theta - F\cos \theta$ , to keep the block at rest.

Hence, the limiting value of frictional force is $mg\sin \theta - F\cos \theta$.

Note: When writing the equation of motion of the block, divide the component of forces carefully. If the frictional force is zero then we have to apply more force on the block to keep it steady else it will start sliding with some acceleration.The normal force will be zero if the sine component of the applied force acts in the opposite direction to the cosine component of the weight. Then only we will have no normal force acting on the body.