Question

A block of wood weighs $10N$ and rests on an inclined plane. The coefficient of friction is $0.7.$ The frictional force that acts on the block when the plane is $30^\circ$ inclined with the horizontal is:
A. $0.062N$
B. $5N$
C. $9.8N$
D. $70N$

Answer 1

Draw a free body diagram and then use newton’s law on the resolved horizontal and vertical components.
${F_{net}} = ma$ where F is the force, m is the mass, a is the acceleration.

Complete step by step answer:

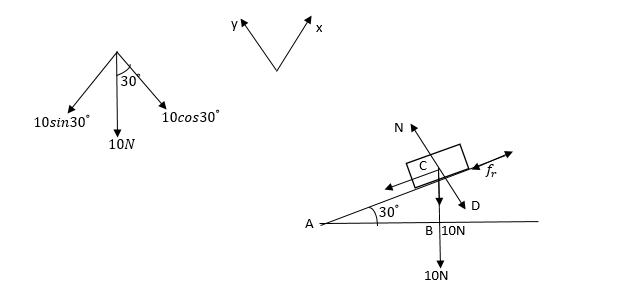
The box is placed on an inclined plane of an inclination $30^\circ .$
The box is at rest means the force of friction is acting opposite to the indication to stop the box from sliding. Let us assume x-axis along the inclinations and y-axis along the perpendicular to the inclinations.
Then, frictional force, ${f_r}$ will act along $+ ve$ x-axis.
Normal force, that is applied by the inclined surface on the box will act along the $+ ve$ y-axis. The weight of the box due to gravitational force will act downward. For simplification, we need to restore the weight along the assumed x and y- axes.
For that consider $\Delta$ABC
$< CAB = 30^\circ$ (Given)
$< ABC = 90^\circ$ (Observe the diagram)
We know that the sum of angles of a triangle is $180^\circ$
$\therefore < CAB + < ABC + < ACB = 180^\circ$
Substituting the values, we get
$30^\circ + 90^\circ + < ACB = 180^\circ$
Rearranging it, we get
$< ACB = 180^\circ - 90^\circ - 30^\circ$
$\Rightarrow < ACB = 90^\circ - 30^\circ$
$\Rightarrow < BCD = 30^\circ$
$\left( {\because < ACD = 90^\circ } \right)$
Therefore, the resolution of weight will be $10\cos {30^\circ }$ along $- ve$ y-axis and $10\sin {30^\circ }$ along negative x-axis.
Now, use Newton's second saw as a projection to solve the question.
We have, ${F_{net}} = ma$
Since the force would act only along x-axis, we have $\sum {{F_x} = ma}$and $\sum {{F_y} = 0}$
Where, $ma$ is the force that is acting on the box to try to slide it downwards.
We will resolve the components along the y-axis.
$\Rightarrow \sum {{F_y} = n - 10\cos 30^\circ = 0}$
Where $+ ve$ and $- ve$ y-axis.
$\Rightarrow N = 10\cos 30^\circ$
$\Rightarrow N = 10 \times \dfrac{{\sqrt 3 }}{2}\left( {\because \cos 30^\circ = \dfrac{{\sqrt 3 }}{2}} \right)$
$\Rightarrow N = 5\sqrt 3 N$
Now, we know that
${F_r} = un$
Where u is the coefficient of friction.
$\Rightarrow {f_r} = 0.7 \times 5\sqrt 3 \left( {\because u = 0.7} \right)$
$\Rightarrow {f_r} = 3.5 \times 1.732\left( {\because \sqrt 3 = 1.732} \right)$
$\Rightarrow {f_r} = 6.062N$

So, the correct answer is “Option A”.

Note:
It is important to understand that the body being at rest does not always mean that no external force is acting on it. It is also possible that some force is being applied on it but that force is not enough to move the body due to higher frictional force acting against it, due to which the body is at rest. If we neglect this concept and write $\sum {{F_x}} = 0$ is this question, then our answer will be $5N$ which is incorrect.