Question

A block of wood floats in water with $\dfrac{4}{5}th$ of its volume submerged, but it just floats in another liquid. The density of liquid is (in $kg/{m^3}$ )
(a) 750
(b) 800
(c) 1500
(d) 1250

Answer 1

Due to buoyant force things float according to law of floatation. Then by applying Archimedes' principle, we can find the density of the liquid.
Formula used:
Archimedes' principle
Weight of the body = weight of liquid displaced.

Complete step by step answer:
Archimedes' principle states that when a body is partially or wholly immersed in a fluid, it experiences an upward thrust equal to the weight of the fluid displaced by it and its upthrust acts through the centre of gravity of the displaced fluid.
Law of floatation: The law of floatation states that a body will float in a liquid if the weight of the liquid displaced by the immersed part of the body is equal to or greater than the weight of the body.

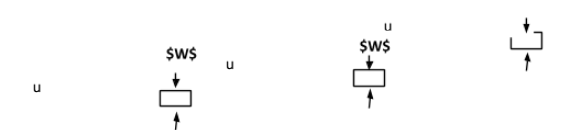
For first case, $\dfrac{4}{5}th$ volume of wood is submerged in water.
Let V be the volume of the block. When block floats in water, then
Weight of block = buoyancy force
$V \times {\rho _{block}} \times g = \left( {\dfrac{{4V}}{5}} \right) \times {\rho _{mater}} \times g$
${\rho _{block}} = \left( {\dfrac{4}{5}} \right){\rho _{water}}$ …………….(i)
When block floats in liquid
Weight of block = $V \times {\rho _{liquid}} \times g$
$V \times {\rho _{block}} \times g\, = V \times {\rho _{liquid}} \times g$
${\rho _{block}} = {\rho _{liquid}}$
${\rho _{liquid}} = \dfrac{4}{5}{\rho _{water}} -$ (from equation (i)
Now, density of water, ${\rho _{water}} = {10^3}Kg/{m^3}$
$= 800\,Kg/{m^3}$
Here, $\rho$ represent density and g is acceleration due to gravity
Hence, option (B) is the correct option.

Note: One must remember that for weight of liquid, density of liquid is to be taken and also,
$Weight = mass \times acceleration\,due\,to\,gravity$
$W = mg$
and density, $\rho = \dfrac{{mass,m}}{{Volume,v}}$
$\rho = \dfrac{m}{v}$
$\Rightarrow m = \rho v$
From here it comes
Weight, w=$\rho \,vg$