Question
Question: A block of weight W produces an extension of \( 9cm \) when it is hung by an elastic spring of lengt...
A block of weight W produces an extension of 9cm when it is hung by an elastic spring of length 60cm and is in equilibrium. The spring is cut into two parts, one of length 40cm and the other of length 20cm . The same load W hangs in equilibrium supported by both parts as shown in the figure. The extension now is:
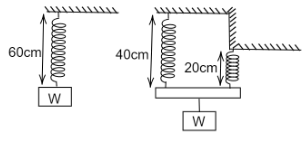
Solution
Hint : The two cut parts of the spring are assumed to be two different springs. In first case they are assumed to be connected in series and in next they are connected in parallel. We can solve for the value of these constants and then calculate the extension produced when they are connected in parallel.
Formula used:
⇒F=kx
In series connection ,
⇒keff1=k11+k21
In parallel connection,
⇒keff=k1+k2
Where keff is the effective spring constant, k1 and k2 are the individual spring constants, x is the extension. F is the restoring force.
Complete step by step answer
It is given in the question that,
The weight of the block is W .
Extension produced in the spring when W is connected is 9cm .
We know that, force in a spring is given by,
⇒F=kx
Where k is the spring constant.
And x is the extension produced in it.
Let the spring constant in the first case be kA
Comparing this with the spring in question,
⇒W=kA×9
⇒kA=9W
This relation shows that k is inversely proportional to the extension.
In the second case the spring is cut into two parts, let their spring constants be k1 and k2 .
Since k is inversely proportional to the length,
⇒k2k1=l1l2
It is given that, l1=40 and l2=20 cm.
⇒k2k1=4020
On simplifying this we obtain,
⇒2k1=k2
For the first case it can be assumed that springs were connected in series (end to end connection),
Adding k1 and k2 as per series connection,
⇒kA1=k11+k21
Or, kA=k1+k2k1k2
Substituting, 2k1=k2 ,
⇒kA=k1+2k12k12=32k1
⇒k1=23kA
Similarly,
⇒k2=2×23kA
⇒k2=3kA
The effective spring constant when both springs are connected in parallel is given by,
⇒kB=k1+k2
In terms of kA ,
⇒kB=(23+3)kA
⇒kB=29kA
For extension,
⇒W=kBx
On substituting the value of W and kB we get,
⇒9kA=29kAx
∴x=2
Therefore the extension produced in the second case is 2cm .
Note
When two or more springs are connected in parallel the effective spring constant is more than the highest value of spring constant, whereas when the springs are connected in series, the effective spring constant is less than the least value of spring constant.
