Question

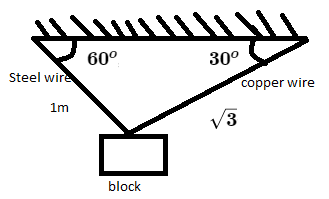
A block of weight $100N$ is suspended by copper and steel wires of same cross sectional area $0.5c{m^2}$ and length $\sqrt 3 m$ and $1m$ respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are ${30^ \circ}$ and ${60^ \circ }$ respectively. If elongation in copper wire is $\left( {\Delta {l_C}} \right)$ and elongation in steel wire is $\left( {\Delta {L_S}} \right)$, then the ratio $\dfrac{{\Delta {l_C}}}{{\Delta {l_S}}}$ is _____. (Young’s modulus for copper and steel are $1 \times {10^{11}}N{m^{ - 2}}$ and $2 \times {10^{11}}N{m^{ - 2}}$, respectively)

Answer 1

Here we apply the Hooke’s law for stress and strain to find the ratio $\dfrac{{\Delta {l_C}}}{{\Delta {l_S}}}$.
The Hooke’s law says that the displacement or scale of the deformation is directly proportional to the deforming force or load for relatively minor deformations of an object.
Hooke’s law also states that the strain of the material beyond the elastic boundary of that material is equal to the stress applied. The atoms and molecules contract as the elastic structures are strained before tension is added and they revert to their original state when the tension is withdrawn.

Complete step by step answer:
Given,
Young’s modulus for copper, ${Y_C} = 1 \times {10^{11}}N{m^{ - 2}}$
Young’s modulus for steel, ${Y_S} = 2 \times {10^{11}}N{m^{ - 2}}$
Length of copper wire, ${L_C} = \sqrt 3 m$
Length of steel wire, ${L_S} = 1m$
Elongation in copper wire is $\left( {\Delta {L_C}} \right)$
Elongation in steel wire is $\left( {\Delta {l_S}} \right)$

The angles subtended by copper and steel wires with ceiling are ${30^ \circ }$ and ${60^ \circ }$.

The cross-sectional area $0.5c{m^2}$ is the same for both copper and steel wires.
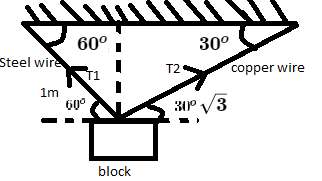
Let ${T_1}$ and ${T_2}$ be the tensional force for steel and copper wire.
Let $A$ be the cross-sectional area.

According to Hooke’s law
Stress = $Y$ × strain
$\dfrac{F}{A} = Y \times\dfrac{{\Delta l}}{l} \\\ \implies \Delta l = \dfrac{{Fl}} {{AY}} \\\$
$\implies \Delta {l_C} = \dfrac{{{T_2} \times {l_C}}}{{A \times {Y_C}}}$ ...... (i)
Force $F$ is equal to the torsional force ${T_2}$ for copper wire
Also,
$\Delta {l_S} = \dfrac{{{T_1} \times {l_S}}}{{A \times {Y_S}}}$ ...... (ii)
Force $F$ is also equal to the torsional force ${T_1}$ for steel wire
Equation (i) divided by equation (ii), we get-
$\dfrac{{\Delta {l_C}}} {{\Delta {l_S}}} = \dfrac{{{T_2}{l_C} \times {Y_S}}} {{{Y_C}{T_1} \times {l_S}}} \\\ = \dfrac{{{Y_S}}} {{{y_C}}} \times \dfrac{{{l_C}}} {{{l_S}}} \times \dfrac{{{T_2}}} {{{T_1}}} \\\$

$\dfrac{{\Delta {l_C}}} {{\Delta {l_S}}} = \dfrac{{2 \times {{10}^{11}}}} {{{{10}^{11}}}} \times \dfrac{{\sqrt 3 }} {1} \times \dfrac{{{T_2}}} {{{T_1}}}$ ...... (iii)
Now applying resultant of horizontal component
$\sum {F_x} = 0 \\\ \implies {T_2}\cos {30^ \circ } - {T_1}\cos {60^ \circ } = 0 \\\ \implies \dfrac{{{T_2}}} {{{T_1}}} = \dfrac{1} {{\sqrt 3 }} \\\$

So, from equation (iii), we get-
$\dfrac{{\Delta {l_C}}} {{\Delta {l_S}}} = \dfrac{{2 \times {{10}^{11}}}} {{{{10}^{11}}}} \times \dfrac{{\sqrt 3 }} {1} \times \dfrac{{{T_2}}} {{{T_1}}} \\\ = 2\sqrt 3 \times \dfrac{1} {{\sqrt 3 }} \\\ = 2 \\\$
Hence,
If elongation in copper wire is $\left( {\Delta {l_C}} \right)$ and elongation in steel wire is $\left( {\Delta {l_S}} \right)$, then the ratio $\dfrac{{\Delta {l_C}}}{{\Delta {l_S}}}$ is $2$.

Note:
Here we have to pay attention that the area is the same for both the wires, so the area gets cancelled. Also the horizontal component will be negative for steel wire.