Question

A block of mass rests on a rough inclined plane making an angle of $30^\circ$ with the horizontal. The coefficient of static friction between the block and the plane is $0.8$. If the frictional force on the block is $10{\text{N}}$, then find the mass of the block in ${\text{kg}}$. Take $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ .
A) $2.0$
B) $4.0$
C) $1.6$
D) $2.5$

Answer 1

As the block of mass rests on an inclined plane which makes some angle with the horizontal, the weight of the block will have components in the horizontal and vertical directions. The normal force acting on the block will be balanced by the cosine component of the weight of the block and the frictional force will be balanced by the sine component of the force.

Complete step by step answer:
Step 1: Sketch a free body diagram of the given arrangement and list the parameters given in the question.

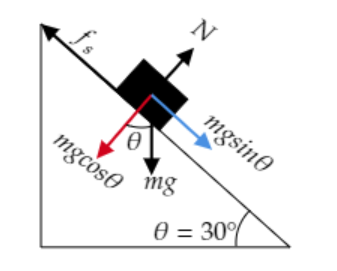
The above figure represents the block of mass $m$ resting on the rough inclined plane which makes an angle $\theta = 30^\circ$ with the horizontal.
The static friction is given to be ${f_s} = 10{\text{N}}$ .
The acceleration due to gravity is given to be $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ .
The coefficient of static friction is given to be ${\mu _s} = 0.8$ .
The weight of the block $W = mg$ is resolved into its cosine component $mg\cos \theta$ and its sine component $mg\sin \theta$ .
As seen from the figure, the forces acting on the block are
1. The cosine component of the weight of the block $mg\cos \theta$
2. The sine component of the weight of the block $mg\sin \theta$
3. Normal force $N$
4. Static friction ${f_s}$

Step 2: Express the force balance equation in the direction of the motion of the block to determine the mass of the block.
The force balance equation along the inclined plane is given as $mg\sin \theta = {f_s}$ .
$\Rightarrow m = \dfrac{{{f_s}}}{{g\sin \theta }}$ -------- (1)
Substituting for ${f_s} = 10{\text{N}}$, $\theta = 30^\circ$, $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ in equation (1) we get, $\Rightarrow m = \dfrac{{10}}{{10 \times \sin 30^\circ }} = 2{\text{kg}}$
Thus the mass of the block is $m = 2{\text{kg}}$ .

So the correct option is (A).

Note: Here the block will slide along the plane once it overcomes the static frictional force. The frictional force will be such that it opposes the motion of the block along the plane and hence will be opposite in direction to the sine component of the weight of the block. We can also obtain the force balance equation in the vertical direction as $N = mg\cos \theta$. The normal force refers to the contact force that is exerted by the plane on the block so that the block does not pass through the plane’s surface. It is a reaction to the weight of the body.