Question

A block of mass $m$ takes time $t$ to slide down a smooth inclined plane of angle of inclination $\theta$ and height $h$. If the same block slides down on a rough inclined plane of same angle of inclination and same height and takes time $n$ times of initial value, then coefficient of friction between block and inclined plane is
A.$\left[ {1 + {n^2}} \right]\tan \theta$
B. $\left[ {1 - \dfrac{1}{{{n^2}}}} \right]\tan \theta$
C. $\left[ {1 - {n^2}} \right]\tan \theta$
D. $\left[ {1 + \dfrac{1}{{{n^2}}}} \right]\tan \theta$

Answer 1

Use the expression for Newton’s second law of motion and the kinematic equation for the displacement. Apply Newton’s second law of motion to the block on a smooth and rough inclined plane in horizontal direction and then determine the time to come down in both cases. Use the given relation between the times for both cases and derive the relation for the coefficient of friction.

Formulae used:
The expression for Newton’s second law of motion is
${F_{net}} = ma$ …… (1)
Here, ${F_{net}}$ is the net force on the object, $m$ is the mass of the object and $a$ is the acceleration of the object.
The kinematic expression for displacement $s$, initial velocity $u$, time $t$ and acceleration $a$ is
$s = ut + \dfrac{1}{2}a{t^2}$ …… (2)

Complete step by step answer:
The block of mass $m$ is sliding down an inclined plane with the angle of inclination $\theta$ and height $h$.

Let $L$ be the length of the inclined plane and $a$ be the acceleration of the block.

The diagram representing the horizontal forces acting on the block is as follows:

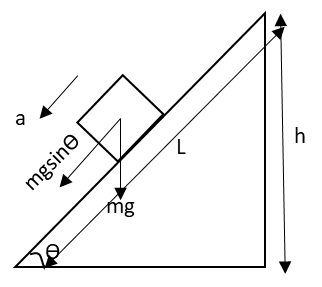
Apply Newton’s second law to the block in the horizontal direction.
$mg\sin \theta = ma$
$\Rightarrow a = g\sin \theta$

Let us determine the sine of angle $\theta$ from the above figure.
$\sin \theta = \dfrac{h}{L}$
$\Rightarrow L = \dfrac{h}{{\sin \theta }}$

Let us now determine the time required for the block to come down.
The initial velocity of the block is zero when it is at rest.

Substitute $L$ for $s$ and $0\,{\text{m/s}}$ for $u$ in equation (2).
$L = \left( {0\,{\text{m/s}}} \right)t + \dfrac{1}{2}a{t^2}$
$\Rightarrow L = \dfrac{1}{2}a{t^2}$
$\Rightarrow t = \sqrt {\dfrac{{2L}}{a}}$ …… (3)

Substitute $\dfrac{h}{{\sin \theta }}$ for $L$ and $g\sin \theta$ for $a$ in the above equation.
$\Rightarrow t = \sqrt {\dfrac{{2\dfrac{h}{{\sin \theta }}}}{{g\sin \theta }}}$
$\Rightarrow t = \sqrt {\dfrac{{2h}}{{g{{\sin }^2}\theta }}}$

This is the expression for the time required for the block to come down on a smooth inclined plane.
Let $\mu$ is the coefficient of friction on the inclined plane.

The diagram representing the horizontal forces acting on the block moving on rough surface is as follows:

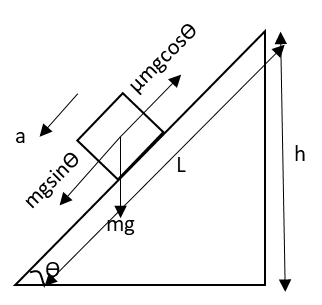
Apply Newton’s second law to the block in the horizontal direction.
$mg\sin \theta - \mu mg\cos \theta = ma$
$\Rightarrow a = g\left( {\sin \theta - \mu \cos \theta } \right)$

Let us now determine the time $t'$ required for the block to slide from the rough inclined plane.
Substitute $t'$ for $t$, $\dfrac{h}{{\sin \theta }}$ for $L$ and $g\left( {\sin \theta - \mu \cos \theta } \right)$ for $a$ in the above equation.
$\Rightarrow t' = \sqrt {\dfrac{{2\dfrac{h}{{\sin \theta }}}}{{g\left( {\sin \theta - \mu \cos \theta } \right)}}}$
$\Rightarrow t' = \sqrt {\dfrac{{2h}}{{g\sin \theta \left( {\sin \theta - \mu \cos \theta } \right)}}}$

We have given that the time $t'$ is $n$ times the time $t$.
$t' = nt$

Substitute $\sqrt {\dfrac{{2h}}{{g\sin \theta \left( {\sin \theta - \mu \cos \theta } \right)}}}$ for $t'$ and $\sqrt {\dfrac{{2h}}{{g{{\sin }^2}\theta }}}$ for $t$ in the above equation.
$\sqrt {\dfrac{{2h}}{{g\sin \theta \left( {\sin \theta - \mu \cos \theta } \right)}}} = n\sqrt {\dfrac{{2h}}{{g{{\sin }^2}\theta }}}$

Take square on both sides of the above equation.
$\dfrac{{2h}}{{g\sin \theta \left( {\sin \theta - \mu \cos \theta } \right)}} = n\dfrac{{2h}}{{g{{\sin }^2}\theta }}$
$\Rightarrow \dfrac{1}{{\left( {\sin \theta - \mu \cos \theta } \right)}} = \dfrac{{{n^2}}}{{\sin \theta }}$
$\Rightarrow \sin \theta = {n^2}\sin \theta - {n^2}\mu \cos \theta$
$\Rightarrow {n^2}\mu \cos \theta = {n^2}\sin \theta - \sin \theta$
$\Rightarrow \mu = \dfrac{{{n^2}\sin \theta }}{{{n^2}\cos \theta }} - \dfrac{{\sin \theta }}{{{n^2}\cos \theta }}$
$\Rightarrow \mu = \tan \theta - \dfrac{1}{{{n^2}}}\tan \theta$
$\Rightarrow \mu = \left[ {1 - \dfrac{1}{{{n^2}}}} \right]\tan \theta$

Therefore, the coefficient of friction is $\left[ {1 - \dfrac{1}{{{n^2}}}} \right]\tan \theta$.

So, the correct answer is option (B).

Note:
The students may apply Newton’s second law of motion in the vertical direction also. But there is no need to apply Newton’s second law of motion in vertical direction as the required coefficient of friction can be derived only by applying the law in horizontal direction.