Question

A block of mass m slides from the rim of a hemispherical bowl of radius R. The velocity of the block at the bottom will be
A. $\sqrt {3Rg}$
B. $\sqrt {2gR}$
C. $\sqrt {Rg}$
D. $\sqrt {4gR}$

Answer 1

When some amount of work is done against the conservative force then the work done will be stored in the system as the potential energy as energy can neither be created nor destroyed. Along the direction of conservative force then potential energy of the system decreases. By using these two principles we will solve the question.
Formula used:
$U = mgh$

Complete answer:
When a block slides from a certain height it will reach the base with certain velocity and it is due to the law of conservation of mechanical energy. Total initial potential energy a block has will be converted into the kinetic energy by the time it reaches the base of the bowl.
The given situation is represented in the below diagram

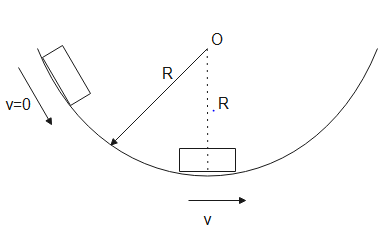
Initially velocity is zero. Except for gravitational force, no other force is acting on the block. So if the block slides down, its potential energy will decrease. The decrease in potential energy will appear as an increase in kinetic energy at the bottom. So as the kinetic energy is increased, its velocity will also increase.
Loss in potential energy is
\eqalign{ & U = mgh \cr & \therefore U = mgR \cr}
Gain in kinetic energy will be
$K = \dfrac{1}{2}m{v^2}$
If we equate both we will get
\eqalign{ & U = K \cr & \Rightarrow mgR = \dfrac{1}{2}m{v^2} \cr & \therefore v = \sqrt {2gR} \cr}

Hence option B is correct.

Note:
Potential energy is valid only if conservative forces are present. Gravity, spring force are the examples for conservative forces. Law of conservation of energy is valid everywhere but the law of conservation of mechanical energy is valid only when no non conservative force acts. Mechanical energy means the sum of potential and kinetic energies.