Question
Question: A block of mass m slides from rest at a height H on a frictionless inclined plane as shown in the fi...
A block of mass m slides from rest at a height H on a frictionless inclined plane as shown in the figure. It travels a distance d across a rough horizontal surface with coefficient of kinetic friction μ, and compresses a spring of spring constant k by a distance x before coming to rest momentarily. Then the spring extends and the lock travels back attaining a final height of h. Then:
A. h=H−2μ(d+x)
B. h=H+2μ(d−x)
C. h=H−2μd+mgkx2
D. h=H−2μ(d+x)
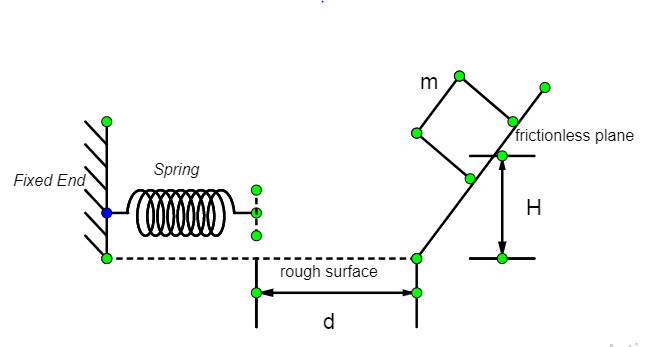
Solution
We can divide the entire motion into 3 parts. First part is the descent on the frictionless surface; second part is the motion on the rough surface and third part is the ascent on the frictionless surface. In all the parts, we apply the conservation of energy equation to obtain height h.
Formula section:
Ki+Pi+Wnc+OEi=Kf+Pf+OEf
Complete step-by-step answer:
The conservation of energy is a classic concept of physics. It states the within a system the total amount of energy remains constant. Energy can neither be created nor be destroyed. The conservation of energy formula is:
Ki+Pi+Wnc+OEi=Kf+Pf+OEf………. (1)
where Kiis initial kinetic energy, Pi is initial potential energy, Wncis work done by non-conservative forces, OEi is other initial energies, Kfis final kinetic energy, Pfis final potential energy, OEf is other final energies.
Let the mass of the block be m.. We can solve the problem by dividing it into three parts.
Part1: The descent of the block on the frictionless incline plane
As the inclined plane is frictionless, work done by non-conservative forces is 0.
Wnc= 0, Ki= 0, Pi= mgH, Kf= K, Pf= 0.
Let’s substitute the above values in equation (1):
0+mgH+0=K+0
⇒K=mgH
Part 2: Motion on the rough surface
External Non conservative force = Friction = -μmg
Distance travelled by the block on the rough surface = 2×(d+x)
Work done Wnc= F dx = -2\times (d+x)$$$$\mu mg
Ki= mgH, Pi= 0, Kf= K, Pf= 0.
Let’s substitute the above values in equation (1):
mgH+0−2×(d+x)×μmg=K+0+0
⇒K=mgH−2×(d+x)×μmg
Part 3: The ascent of the block on the frictionless incline plane
Non conservative forces = 0
Ki=mgH−2×(d+x)×μmg, Pi= 0, Kf= 0, Pf= mgh
Let’s substitute the above values in equation (1):
mgH−2×(d+x)×μmg+0=0+mgh
On dividing the above equation by mg, we get
h=H−2μ(d+x)
Hence the correct option is (A).
Note: The possibility of the mistake is that you may choose option (B) because you may forget that the friction force is an opposing force so the magnitude is –ve. It is important to remember this otherwise you will get option (B).
