Question

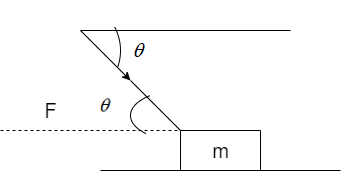
A block of mass m slides along a surface where $\mu$is the coefficient of kinetic friction. A man pushes the block with a force F which makes an angle$\theta$with the horizontal as shown below. The block moves with constant velocity v. Power delivered by the man is:

A) $0$
B) $[F.v\cos \theta ]$
C) $[F\cos \theta - \mu (mg + F\sin \theta )]v$
D) $[F\cos \theta + \mu (mg + F\sin \theta )]v$$$

Answer 1

Recall that the frictional force is defined as the force that opposes the motion of the object when two surfaces are in contact with each other. The frictional force always acts in a direction opposite to the direction of motion of the object. It also varies with the type of surface of the object.

Complete step by step solution:
Since force is a vector quantity, it will have two components. One in horizontal direction which is $F\cos \theta$ and the other is vertical component which is $F\sin \theta$.
Also the normal force N will act in an upward direction and the weight ‘mg’ will act in a downward direction.
Also the coefficient of friction is given by the formula,
$\mu = \dfrac{F}{N}$
Where F is the frictional force
And N is the normal force
$F = \mu N$---(i)
The component of force along horizontal direction is $F\cos \theta$.
$\therefore$equation (i) can be written as
$F\cos \theta - \mu N = 0$---(ii)
The normal force is balanced by the vertical component of force and weight ‘mg’ as they are acting in an opposite direction to the force. Therefore, it can be written as
$\Rightarrow N = mg + F\sin \theta$---(iii)
Substituting the value of N from equation (iii) in equation (ii),
$\Rightarrow F\cos \theta - \mu [mg + F\sin \theta ] = 0$---(iv)
When an object is moving with a constant velocity with some applied force, the formula for power is written as
$Power = Force \times Velocity$
Substituting the value of force, from equation (iv)
$\Rightarrow P = [F\cos \theta - \mu (mg + F\sin \theta )]v$
The power delivered by the man is
$\Rightarrow P = [F\cos \theta - \mu (mg + F\sin \theta )]v$

Option (C) is the right answer.

Note: It is important to remember that the coefficient of friction is the ratio of frictional force and the normal force. When there is a lot of friction between the two surfaces, then the value of coefficient of friction is high. It measures how one object moves in relation to another object in contact.