Question
Question: A block of mass m rigidly attached with a spring k is compressed through a distance A. If the block ...
A block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released the period of oscillation of the block for a complete cycle is equal to
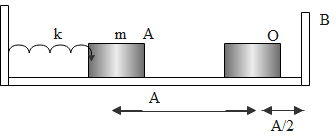
(A)34πkm(B)2πkm(C)32πkm
(D) None of these
Solution
The period of a block of mass m and spring constant k is directly proportional to the square root of its mass and inversely proportional to the square root of spring constant. The time period depends on these two factors. It doesn’t depend on the amplitude. Thus the period of oscillation is the number of oscillations in the total time taken.
Complete step-by-step solution
T=2πkm
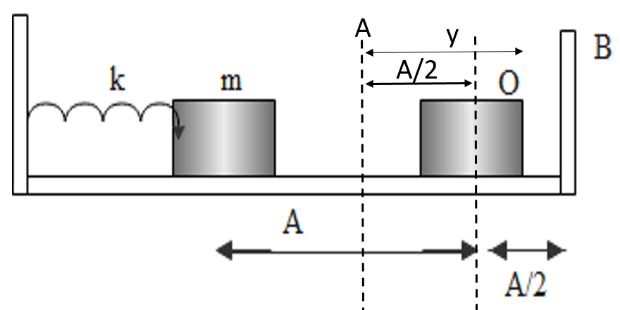
The period of motion from A to O is equal to quarter of the time period T of oscillation of mass spring system as here the total distance traveled during one harmonic motion will be,
x=2(A+21A)x=3A
Distance between point A and O is,
y=(41A+21A)y=43A=4x
So,
tAO=4T
⇒tAO=41[2πkm]
∴tAO=2πkm
Since it is a SHM
OB=OAsinT2πTOB
where, tOB is the time taken from O to B.
tOB=2πTsin−1A2A=6πkm
Hence total time is,
t=2(tAO+tOB)
⇒t=2(2πkm+6πkm)⇒t=34πkm
Hence, option (A) is correct.
Additional information: When the value of the spring constant increases, that will decrease the time period since these two quantities are inversely proportional. And the time period increases with increase in mass since it is directly proportional.
Thus the period is inversely proportional to the square root of spring constant and directly proportional to the square root of the mass of the block. . The time period depends upon these two factors. It doesn’t depend on the amplitude. Thus the period of oscillation is the number of oscillations in the total time taken.
According to Hooke’s law the force is directly proportional to the displacement. Here k the spring constant is the proportionality constant.
Note: Thus the period is inversely proportional to the square root of spring constant and directly proportional to the square root of the mass of the block. . The time period depends upon these two factors. It doesn’t depend on the amplitude. Thus the period of oscillation is the number of oscillations in the total time taken. When the value of the spring constant increases, that will decrease the time period since these two quantities are inversely proportional. And the time period increases with increase in mass since it is directly proportional.
