Question

A block of mass m rests on a rough horizontal surface as shown in the figure. Coefficient of friction between the block and the surface is $\mu$ . A force $F=mg$ acting on angle $\theta$ with the vertical side of the blocks pulls it. In which of the following cases can the block be pulled along the surface?
(A) $\tan \theta \ge \mu$
(B) $\cot \theta \ge \mu$
(C) $\tan \dfrac{\theta }{2}\ge \mu$
(D) $\cot \dfrac{\theta }{2}\ge \mu$

Answer 1

Block can be pulled only when the horizontal components of the force is greater than the force of friction. The vertical components of force will decrease the weight and the normal reaction.
Friction is a force that acts in order to resist relative motion between two surfaces in contact. As the applied force is increased, the magnitude of friction also increases equally to resist motion. However, once friction reaches its maximum value, it cannot resist motion anymore and the block will begin to accelerate. The friction value remains at the maximum value.

Complete step by step solution
As shown in the figure the Normal reaction N on the block and vertical components of the force F are opposite to weight. Vertical motion is balanced, that is net force in vertical direction is zero.
Resolve the components of force into $F\sin \theta$ in the direction of motion and $F\cos \theta$ in the direction of Normal reaction.

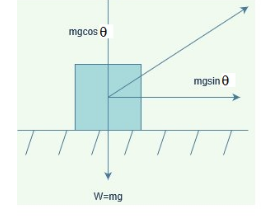
Net force in vertical direction is zero that is
$N+F\cos \theta =Mg$
Or
$N+F\cos \theta -Mg=0$ , $N=Mg-F\cos \theta$
Put $F=Mg$ as given in the question, so by putting we get
$N=Mg-Mg\cos \theta =Mg\left( 1-\cos \theta \right)$
Now putting another condition to make F able to pull the block horizontally $F\sin \theta$ should be greater than or equal to the static friction. We know that the maximum value of the static friction is $\mu N$ .
So, we have
$F\sin \theta \ge \mu N$
Putting value of N we get
$F\sin \theta \ge \mu Mg\left( 1-\cos \theta \right)$
Put the value of F also and the equation becomes
$Mg\sin \theta =\mu Mg\left( 1-\cos \theta \right)$
$\sin \theta =\left( 1-\cos \theta \right)\mu$
Put $\cos \theta =1-2{{\sin }^{2}}\theta and\sin \theta =2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}$
$2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}=\mu \left( 1-\left( 1-{{\sin }^{2}}\dfrac{\theta }{2} \right) \right)$
$\dfrac{\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}}{\sin \dfrac{\theta }{2}\sin \dfrac{\theta }{2}}\ge \mu$
$\therefore$ $\cot \dfrac{\theta }{2}\ge \mu$
Option (D) is correct.

Note
We may classify friction in two types:
-External friction: which arises when two bodies in contact with each other try to move or there is an actual relative motion with two. The external friction is also called contact friction.
-Internal friction: Which arises on account of relative motion between every two layers of a liquid. It is also called viscosity of the liquid.