Question

A block of mass ‘m’ rests on a rough floor. The coefficient of friction between the floor and the block is ‘μ’.
(a). Two boys apply force ‘P’ at an angle θ to the horizontal. One of them pushes the block, the other one pulls. Which one would require less efforts to cause impending motion of the block?
(b). What is the minimum force required to move the block by pulling it?
(c). Show that if the block is pushed at a certain angle ${\theta _{\text{o}}}$, so that it cannot be moved. Then what will be the value of P?

Answer 1

- Hint: In order to find the answer for the given, we start off by drawing the free body diagram of the block when it’s being pushed and pulled. We calculate the force acting on it in both cases. Frictional force on a block always acts in the direction opposite to its direction of motion.
Write components of force P acting on the block.

Formula Used:
Frictional Force F = μN, where μ is the coefficient of friction and N is the normal force acting on the body.

Complete step-by-step solution -

PULLING -
When a body of mass ‘m’ is being pulled with a force ‘P’, its free body diagram looks like:

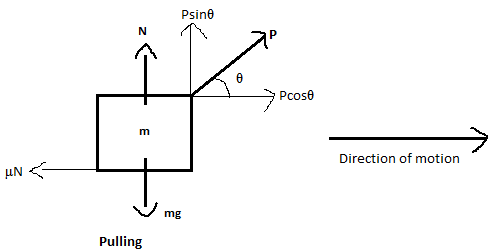
The body is subject to a force of gravity ‘mg’ downwards and the normal force ‘N’ acting opposite to it. The force P acts on the body, away from it at an angle θ. This force P is resolved into components Psinθ and Pcosθ respectively as shown in the figure.
Since the body is being pulled the effective direction of motion of the body should be in horizontal direction as shown in the figure. This causes a frictional force acting on the body opposing its direction of motion which is given by F = μN.
Now we balance all the forces acting on the body in the horizontal and the vertical directions.
In the vertical direction,
N = mg – Psinθ -- (1)
In the horizontal direction,
Pcosθ – μN = 0
Substituting the value of N from equation (1) in the above equation we get,
⟹Pcosθ = μ (mg – Psinθ)
$\Rightarrow {{\text{F}}_{{\text{net1}}}}{\text{ = P = }}\dfrac{{\mu {\text{mg}}}}{{{\text{cos}}\theta {\text{ + }}\mu {\text{sin}}\theta }}$ --- (4)

PUSHING –
When a body of mass ‘m’ is being pushed with a force ‘P’, its free body diagram looks like:

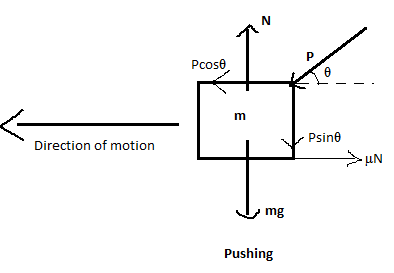
The body is subject to a force of gravity ‘mg’ downwards and the normal force ‘N’ acting opposite to it. The force P acts on the body, towards it at an angle θ. This force P is resolved into components Psinθ and Pcosθ respectively as shown in the figure.
Since the body is being pushed the effective direction of motion of the body should be in horizontal direction as shown in the figure. This causes a frictional force acting on the body opposing its direction of motion which is given by F = μN.
Now we balance all the forces acting on the body in the horizontal and the vertical directions.
In the vertical direction,
N = mg + Psinθ -- (2)
In the horizontal direction,
Pcosθ – μN = 0
Substituting the value of N from equation (2) in the above equation we get,
⟹Pcosθ = μ (mg + Psinθ)
$\Rightarrow {{\text{F}}_{{\text{net2}}}}{\text{ = P = }}\dfrac{{\mu {\text{mg}}}}{{{\text{cos}}\theta {\text{ - }}\mu {\text{sin}}\theta }}$ --- (3)

(a). Let us consider the net force acting on the block of mass ‘m’ when it is both pushed and pulled from equations (3) and (4) respectively:
$\Rightarrow {{\text{F}}_{{\text{net1}}}}{\text{ = P = }}\dfrac{{\mu {\text{mg}}}}{{{\text{cos}}\theta {\text{ + }}\mu {\text{sin}}\theta }}$
$\Rightarrow {{\text{F}}_{{\text{net2}}}}{\text{ = P = }}\dfrac{{\mu {\text{mg}}}}{{{\text{cos}}\theta {\text{ - }}\mu {\text{sin}}\theta }}$
Here the numerator is equal in both cases, the denominator in the net force while pulling$\left( {{{\text{F}}_{{\text{net1}}}}} \right)$ is greater than that of that of pushing$\left( {{{\text{F}}_{{\text{net2}}}}} \right)$. That makes the value of net force ${{\text{F}}_{{\text{net1}}}}{\text{ < }}{{\text{F}}_{{\text{net2}}}}$. Hence the effort required to pull a block is less than the effort required to push it in order to create an impending motion.

(b). The minimum force required by the block to pull it
The effective force while pulling a block is${{\text{F}}_{{\text{net1}}}}{\text{ = P = }}\dfrac{{\mu {\text{mg}}}}{{{\text{cos}}\theta {\text{ + }}\mu {\text{sin}}\theta }}$.
For this force to be minimum, its denominator should be at its maximum value.
I.e. cosθ + μsinθ should be maximum.
We know the function cosθ + sinθ has its maximum value when θ = 45°.
Therefore the maximum value of cosθ + μsinθ is cos 45° + μsin45° = $\dfrac{{1 + \mu }}{{\sqrt 2 }}$.
(We know cos45° = sin45° = $\dfrac{1}{{\sqrt 2 }}$)
The minimum force required to move the block while pulling is ${{\text{F}}_{{\text{min}}}}{\text{ = }}\dfrac{{\sqrt 2 \mu {\text{mg}}}}{{{\text{1 + }}\mu }}$

(c). Pushed at a certain angle ${\theta _{\text{o}}}$, so that it cannot be moved
The net force acting on the body should be less than that required to just move the block, so that the block does not move,
∴${\text{P < }}\dfrac{{\mu {\text{mg}}}}{{{\text{cos}}\theta {\text{ - }}\mu {\text{sin}}\theta }}$ -- from equation (3)

Note – In order to answer this type of question the key is to know how to appropriately draw a free body diagram and depict all forces acting on a body.
Frictional force is defined as the force that opposes relative motion of an object. It depends on the physical attributes of the body and the coefficient of friction of the surface. It occurs in liquids in between the molecules.
Normal force is the force exerted on an object with respect to another object it is in contact with. It is perpendicular to the surface the body is placed on.