Question

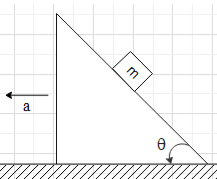
A block of mass m resting on a wedge of angle $\theta$ as shown in the figure. The wedge is given an acceleration ‘a’ towards the left. What is the minimum value of a due to an external agent so that the mass m falls freely?

A. g
B. $g\cos \theta$
C. $g\cot \theta$
D. $g\tan \theta$

Answer 1

The block will be in free fall when the normal force exerted by the wedge is zero. Analyse the situation with respect to the wedge and find an expression for the normal force in terms of ‘a’. Then it goes to zero and finds the minimum value of ‘a’.

Complete step by step answer:
It is given a block of mass m resting on a wedge. Then with external agents, the wedge is accelerated with an acceleration towards the left, as shown. We are asked to find the minimum value of a so that the mass m falls freely. Let us first understand what is free falling. A body is in free fall when it is under the gravitational force only.

In this case, the forces on the block are the gravitational force and the normal force exerted by wedge. Therefore, the block will be in free fall when the normal force exerted by the wedge is zero.Let's analyse the situation with respect to the wedge. With respect to the wedge, in addition to the two forces there will be a pseudo force acting on the block towards right.The magnitude of the pseudo force will be equal to $ma$.

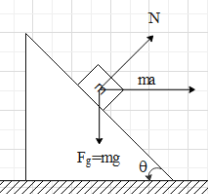
Now, looking at the figure, let us resolve the forces as shown below.

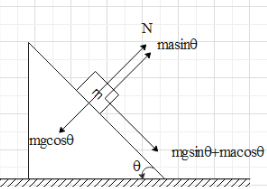
Since the block is in contact with the wedge, the acceleration along the normal to the incline is zero.And from Newton’s 2nd law of motion we know that ${{F}_{net}}=m{{a}_{net}}$.
Therefore, net force on the block in the direction of the normal to the incline is zero.And from the figure we get that the net force along the normal is ${{F}_{net}}=ma\sin \theta +N-mg\cos \theta$.
But ${{F}_{net}}=0$.
$\Rightarrow ma\sin \theta +N-mg\cos \theta =0$
$\Rightarrow ma\sin \theta +N=mg\cos \theta$ …. (i)
We have already discussed that the block will fall freely when the normal force is zero.
Therefore, put $N=0$ in (i).
$\Rightarrow ma\sin \theta +0=mg\cos \theta$
$\Rightarrow a\sin \theta =g\cos \theta$
$\therefore a=g\dfrac{\cos \theta }{\sin \theta }=g\cot \theta$.
This means that for the values of ‘a’ less than $g\cot \theta$, the block is in contact with the wedge and once the value of a is greater than $g\cot \theta$, the block falls freely.Therefore, the minimum value of ‘a’ for the block to fall freely is $g\cot \theta$

Hence, the correct option is C.

Note: The force $ma$ is a pseudo force, which means that it is a false force and does not exist in reality. It is the force acting on the block according to the wedge. A pseudo force comes into play when we deal with relative motion between two bodies.