Question
Question: A block of mass \[m\] moving with velocity \(v\) collides with another stationary block of mass m as...
A block of mass m moving with velocity v collides with another stationary block of mass m as shown. The maximum compression in the spring is ?
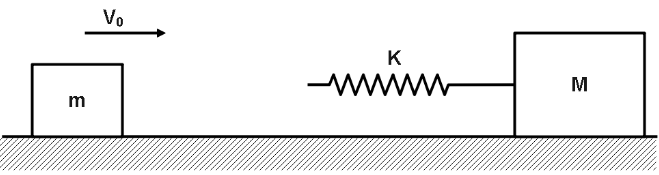
Solution
To solve this question here we will apply energy conservation and also, we know about the spring force and using this law of conservation of energy of the system and formulas of kinetic energy and potential energy we will find the maximum compression.
Formula used:
Espring=21kx2
Where, Espring is the energy of spring, k is the spring constant and x is the length of compression or expansion.
Complete step by step answer:
According to the question, the spring attached with a block of mass M will compress until both the particles start to move together. So, external force acting on the system is 0.Therefore, initial momentum is equal to final momentum
