Question

A block of mass m lying on a horizontal surface (coefficient of static friction= ${\mu _s}$) is to be brought into motion by a pulling Force F. At what angle $\theta$ with the horizontal should the force F be applied so that its magnitude is minimum? Also find its magnitude.

Answer 1

For problems like these we have to first draw the free body diagram, this will help us to better analyze all the forces that are acting on the body. Then once we have drawn the free body diagram if we equate the forces according to vertical and horizontal directions, we can easily calculate the desired values.

Complete answer:
A coefficient of friction is the ratio of the normal reaction between the two bodies involved in the friction.
Let us first draw the free body diagram of the whole scenario.

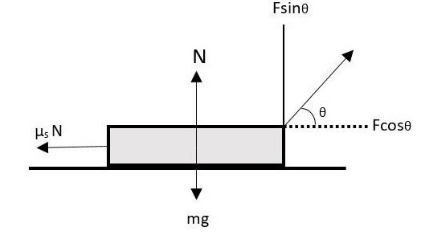
Now, from the free body diagram for the vertical components, we can write,
$\Rightarrow$ $N + F\sin \theta = mg$
Thus, we have
$\Rightarrow$ $N = mg - F\sin \theta$
Similarly, for the horizontal components we have,
$\Rightarrow$ $F\cos \theta = {\mu _s}N$
Now, putting the value of N we have,
$\Rightarrow$ $F\cos \theta = {\mu _s}\left( {mg - F\sin \theta } \right)$
Simplifying we get,
$\Rightarrow$ $F\cos \theta + {\mu _s}F\sin \theta = {\mu _s}mg$
To calculate F we can write,
$\Rightarrow$ $F\left( \theta \right) = \dfrac{{{\mu _s}mg}}{{\cos \theta + {\mu _s}\sin \theta }}$
Again, for the free body diagram we have,
$\Rightarrow$ $\dfrac{{dF}}{{d\theta }} = 0$
Thus, we can equate the previous equation as,
$\Rightarrow$ $F\left( \theta \right) = \dfrac{{{\mu _s}mg}}{{\cos \theta + {\mu _s}\sin \theta }}$
Differentiating we have,
$\Rightarrow$ $\dfrac{{dF}}{{d\theta }} = \dfrac{d}{{d\theta }}\left( {\dfrac{{{\mu _s}mg}}{{\cos \theta + {\mu _s}\sin \theta }}} \right)$
Putting the values, we get
$\Rightarrow$ $0 = \dfrac{d}{{d\theta }}\left( {\dfrac{{{\mu _s}mg}}{{\cos \theta + {\mu _s}\sin \theta }}} \right)$
Further simplifying we get,
$\Rightarrow$ ${\mu _s} = \tan \theta$
Thus, we have from equating the above equation,
$\Rightarrow$ $\theta = {\tan ^{ - 1}}\left( {{\mu _s}} \right)$
Thus, the minimum value of the force will be at angle $\theta = {\tan ^{ - 1}}\left( {{\mu _s}} \right)$.
Again, we have
$\Rightarrow$ $F = \dfrac{{{\mu _s}mg}}{{\cos \theta + {\mu _s}\sin \theta }}$
Dividing the denominator and numerator of the right-hand side with $\cos \theta$, we have
$\Rightarrow$ $F = \dfrac{{\dfrac{{{\mu _s}mg}}{{\cos \theta }}}}{{\dfrac{{\cos \theta + {\mu _s}\sin \theta }}{{\cos \theta }}}}$
This gives us,
$\Rightarrow$ $F = \dfrac{{\dfrac{{{\mu _s}mg}}{{\cos \theta }}}}{{1 + {\mu _s}\tan \theta }}$
Substituting ${\mu _s} = \tan \theta$we get,
$\Rightarrow$ $F = \dfrac{{\dfrac{{{\mu _s}mg}}{{\cos \theta }}}}{{1 + {\mu _s}^2}}$
Again, using the value of $\theta$ and using Pythagoras theorem we have,
$\Rightarrow$ $\cos \theta = {\left( {1 + {\mu _s}^2} \right)^{ - \dfrac{1}{2}}}$
Thus, putting this value, we have,
$\Rightarrow$ $F = \dfrac{{{\mu _s}mg}}{{1 + {\mu _s}^2}}{\left( {1 + {\mu _s}^2} \right)^{\dfrac{1}{2}}}$
Further simplification gives us,
$\Rightarrow$ $F = \dfrac{{{\mu _s}mg}}{{{{\left( {1 + {\mu _s}^2} \right)}^{\dfrac{1}{2}}}}}$

Thus, the magnitude of the force that is to be applied is $\dfrac{{{\mu _s}mg}}{{{{\left( {1 + {\mu _s}^2} \right)}^{\dfrac{1}{2}}}}}$.

Note:
The problems sometimes need further simplification which can be done with the help of basic theorems like the Pythagoras theorem we used in this particular problem to get the value of $\cos \theta$.