Question

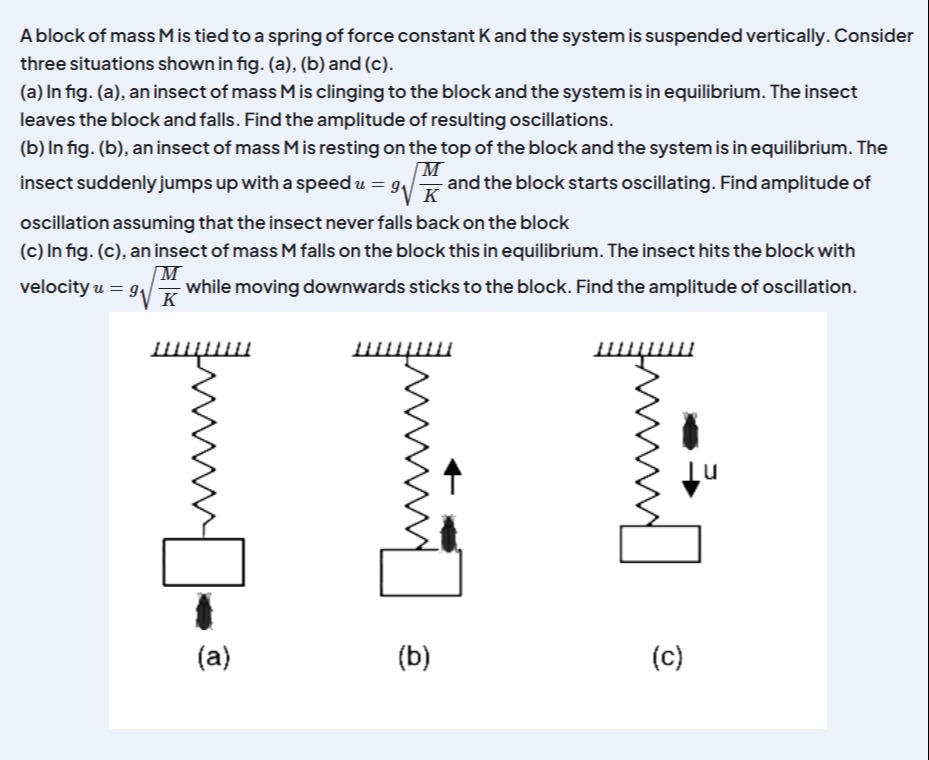
A block of mass M is tied to a spring of force constant K and the system is suspended vertically. Consider three situations shown in fig. (a), (b) and (c).

(a) In fig. (a), an insect of mass M is clinging to the block and the system is in equilibrium. The insect leaves the block and falls. Find the amplitude of resulting oscillations.

(b) In fig. (b), an insect of mass M is resting on the top of the block and the system is in equilibrium. The insect suddenly jumps up with a speed $u = 9\sqrt{\frac{M}{K}}$ and the block starts oscillating. Find amplitude of oscillation assuming that the insect never falls back on the block

(c) In fig. (c), an insect of mass M falls on the block this in equilibrium. The insect hits the block with velocity $u = 9\sqrt{\frac{M}{K}}$ while moving downwards sticks to the block. Find the amplitude of oscillation.

Answer 1

A_a = Mg/K, A_b = (M/K)sqrt(g^2 + 81/4), A_c = (M/K)sqrt(g^2 + 81/2)

Answer 2

The problem involves finding the amplitudes of oscillation in three different scenarios. Here's a breakdown of the solutions:

(a) Insect Leaves the Block

• Initially, the system (block + insect) is in equilibrium. The spring is extended due to the combined weight.
• When the insect leaves, the equilibrium position shifts. The block oscillates around this new position.
• The amplitude of oscillation is equal to the difference between the initial and final equilibrium positions, which is $\frac{Mg}{K}$.

(b) Insect Jumps Off the Block

• Initially, the system is in equilibrium with the insect resting on the block.
• The insect jumps upwards with a given speed.
• Using conservation of momentum, the velocity of the block immediately after the jump is calculated.
• The amplitude of oscillation is then calculated using the energy equation for SHM, considering both the displacement from the new equilibrium position and the initial velocity.
• The final amplitude is $\frac{M}{K} \sqrt{g^2 + \frac{81}{4}}$.

(c) Insect Falls and Sticks to the Block

• Initially, the block is in equilibrium.
• The insect falls and sticks to the block. This is an inelastic collision.
• Using conservation of momentum, the velocity of the combined system (block + insect) immediately after the collision is calculated.
• The amplitude of oscillation is then calculated using the energy equation for SHM.
• The final amplitude is $\frac{M}{K} \sqrt{g^2 + \frac{81}{2}}$.