Question

A block of mass $m$ is suspended by different springs of force constant shown in figure. Let the time period of oscillations in these four positions be $T_1$ , $T_2$ , $T_3$ , and $T_4$ . Then
(i)
(ii)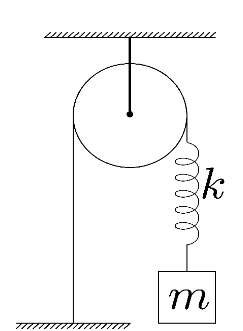
(iii)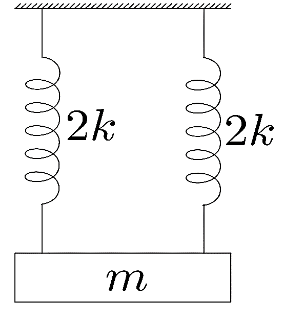
(iv)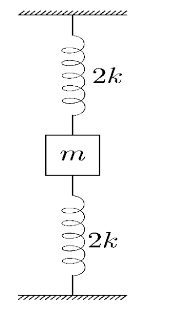

A. ${{T}_{1}}={{T}_{2}}={{T}_{4}}$
B. ${{T}_{1}}={{T}_{2}}$ and ${{T}_{3}}={{T}_{4}}$
C. ${{T}_{1}}={{T}_{2}}={{T}_{3}}$
D. ${{T}_{1}}={{T}_{3}}$ and ${{T}_{2}}={{T}_{4}}$

Answer 1

To find the relation between the time periods of the given positions, we will find the time period of each position separately using the formula of time period of oscillations. For the cases with more than one spring, first we need to understand the arrangement, whether they are in series or parallel arrangement, find the equivalent spring constant and then the time period of oscillation.

Formula Used:
Time period of oscillation $T=2\pi \sqrt{\dfrac{m}{k}}$ , where $T$ is the time period of oscillation, $m$ is the mass of the object attached to the spring, $k$ is the spring constant.

Complete step by step answer:
(i) Here, we are given different arrangements for the spring-mass system. Let us consider each arrangement individually. In the first case, we are given a spring of spring constant $k$ and a block of mass $m$ attached to the spring through a pulley. But we know that the time period of oscillation depends only on the mass of the block and the spring constant.
Hence, the pulley plays no role in the time period of oscillation. Hence, for this arrangement the time period of oscillation can be calculated as
${{T}_{1}}=2\pi \sqrt{\dfrac{m}{k}}$ …… $(1)$

(ii) In the second case, we are given a spring of spring constant $k$ and a block of mass $m$ attached to the spring that is held to a base through a pulley. But we know that the time period of oscillation depends only on the mass of the block and the spring constant.
Hence, the pulley play no role in the time period of oscillation. Hence, for the arrangement the time period of oscillation can be calculated as
${{T}_{2}}=2\pi \sqrt{\dfrac{m}{k}}$ …… $(2)$

(iii) In the third case, we are given two springs with spring constant $k$ each and a single block connected to both the springs of mass $m$ . Here, as we are given two springs, we need to find an equivalent spring constant. Hence, we need to understand whether the arrangement of the springs is series or parallel. Here, in the given arrangement, if we pull the block downwards the springs will get stretched by a length say $y$.

As both the springs are attached to the same block, both the springs will get stretched by the same length. Hence, as the extension is same, the springs are said to be attached in parallel arrangement and the equivalent spring constant can be calculated as
${{k}_{eq}}=2k+2k=4k$
Hence, substituting the equivalent spring constant and the mass in the equation of time period of oscillation we get,
${{T}_{3}}=2\pi \sqrt{\dfrac{m}{{{k}_{eq}}}}$
$\therefore {{T}_{3}}=2\pi \sqrt{\dfrac{m}{4k}}$
Applying square root on the number, we get
${{T}_{3}}=\dfrac{2\pi }{2}\sqrt{\dfrac{m}{k}}$
$\therefore {{T}_{3}}=\pi \sqrt{\dfrac{m}{k}}$ …… $(3)$

(iv) In the fourth case, we are given two springs with spring constant $k$ each and a single block connected to both the springs of mass $m$ . Here, as we are given two springs, we need to find an equivalent spring constant.Hence, we need to understand whether the arrangement of the springs is series or parallel.

Here, in the given arrangement, if we pull the block downwards the spring above the block will get stretched and the spring below the block will get compressed. But as both springs are attached to the same block the extension and the compression will be equal to say $y$.Hence, as the extension in the spring above the block and the compression in the spring below the block is same, the springs are said to be attached in parallel arrangement and the equivalent spring constant can be calculated as
${{k}_{eq}}=2k+2k=4k$

Hence, substituting the equivalent spring constant and the mass in the equation of time period of oscillation we get,
${{T}_{4}}=2\pi \sqrt{\dfrac{m}{{{k}_{eq}}}}$
${{T}_{4}}=2\pi \sqrt{\dfrac{m}{4k}}$
Applying square root on the number, we get
${{T}_{4}}=\dfrac{2\pi }{2}\sqrt{\dfrac{m}{k}}$
$\therefore {{T}_{4}}=\pi \sqrt{\dfrac{m}{k}}$ …… $(4)$
Hence, from the equations $(1)$ , $(2)$ , $(3)$ , and $(4)$ , we can obtain the relation between the time periods as $T_1=T_2$ and $T_3=T_4$

Hence, the correct answer is option B.

Note: Here, we need to understand that the time period of oscillation depends only on the spring constant of the spring and the mass of the object attached. It is not affected in any way by its arrangement. Hence, the pulleys and the length of string between the block and the spring does not affect the time period of oscillation.