Question
Question: A block of mass \(m\) is resting on a smooth horizontal surface. One end of a uniform rope of mass \...
A block of mass m is resting on a smooth horizontal surface. One end of a uniform rope of mass 3m is fixed to the block, which is pulled in the horizontal direction by applying force F at the other end. The tension in the middle of the rope is:
A. 68F
B. 71F
C. 81F
D. 87F
Solution
Hint: This problem can be solved by considering the block and one half of the rope attached to the block as one system and the other half of the rope as the other system and applying force balance equations on the two systems. Since, the rope is uniform, half of the rope will have half of the mass of the total rope.
Formula used:
The force F exerted by or on a body is the product of the mass of the body m and the acceleration a produced in the body in the direction of that force due to it. That is,
F=ma
Complete step-by-step answer:
Since we have to find the tension in the rope at the midpoint, we will virtually break the rope in two halves to make two systems. One system will consist of the rope connected with the block and the other system will be the other half of the rope which is being pulled by the force F.
Since, the rope is uniform, it must have a constant mass per unit length. Hence, half of the rope will have half of the mass of the total rope. Therefore, since the mass of the total rope is 3m, the mass of half of it will be 21×3m=6m --(1)
We will only solve in the horizontal axis, since there is equilibrium in the vertical axis.
Let us draw the free body diagrams of the two systems.
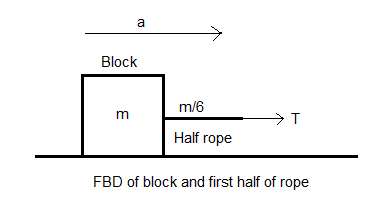
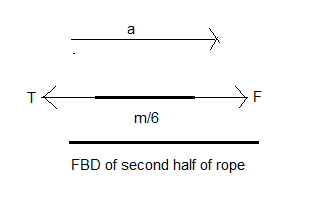
Since the rope is inextensible, both the parts of the rope must have the same acceleration in the same direction. Let this acceleration be a. Now, T is the tension in the middle of the rope. By Newton’s third law which states that when a body applies a force on another body the latter exerts the same magnitude of force in the opposite direction on the first body.
Hence, the first half of the rope gets a force T from the second half in the direction shown and in turn pulls the second half with the same magnitude but in the opposite direction as shown in the free body diagram (FBD).
Now, the force F exerted by or on a body is the product of the mass of the body m and the acceleration a produced in the body in the direction of that force due to it. That is,
F=ma --(2)
The total mass of the (block and half rope) system will be m+6m=67m --(3) [Using (1)]
Let us apply (2) on the first system (block and half rope)
T=67ma [Using (3)] ∴a=7m6T --(4)
Now, let us apply (2) on the second system, F−T=6ma Now, putting (4) in the above equation, we get, F−T=6m×7m6T=7T
∴F=7T+T=78T
∴T=87F
Therefore, the required tension in the middle of the rope is 87F.
Therefore, the correct option is D) 87F.
Note: Students often forget to consider the mass of the rope in such questions. If the mass of the rope is not considered, then the tension will be uniform throughout the length of the rope. It is the mass of the rope that is causing the tension in the rope to vary along its length. Questions are sometimes set up purposefully to check whether the student can catch this point or not.
It is always good to break the total problem into the required number of parts and systems and draw individual free body diagrams for each. This gives a lot more clarity as to what the question requires and gives a better understanding of the problem.
