Question

A block of mass m is resting on a piston as shown in the figure which is moving vertically in a SHM of period 1 s. The minimum amplitude of motion at which the block and piston separate is :
A. 0.25 m
B. 0.52 m
C. 2.5 m
D. 0.15 m

Answer 1

At first we have to draw the diagram required for the question that is as given in the question. Now we have to find the amplitude from the derived formula of angular acceleration. Here we see that a mass m is placed on the block now when the block is placed the air pressure inside the container tends to push it back upwards now this results in a to and fro motion of the piston as once the weight of the mass works and at other time the upwards pressure works that’s why the body is in SHM.

Formula used:
${{\omega }^{2}}A=\left( \dfrac{2\pi }{T} \right)A=g$,
$Amplitude(A)=\dfrac{Maximum\text{ }velocity({{V}_{\max }})}{\omega }$

Complete answer:
According to the question, the diagram should be

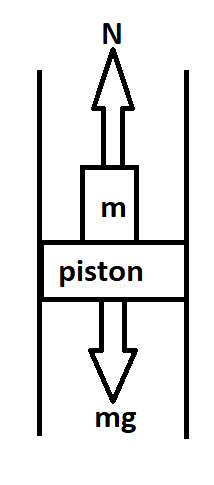
Here, in the above diagram we see a piston on which a block of mass ‘m’ is placed and the piston is opposing the force given by the block with a force N we can say this N is angular acceleration as this motion exhibited is a simple harmonic motion, and the block is pushing the piston down with its mass and gravity that is ‘mg’.
So according to the question, it is asked to find the minimum amplitude of motion at which the piston will just move down from the block and the block will be in air.
Now, we can say that,
N = g (gravitational force)
We know that angular acceleration is,
${{\omega }^{2}}A=\left( \dfrac{2\pi }{T} \right)A=g$ ,
Now we have to find the amplitude, so we know that time period T = 1 sec.
On solving we get,
$A=0.248m$ this is the amplitude.
Now we are asked to find the maximum velocity,
We know that,
$Amplitude(A)=\dfrac{Maximum\text{ }velocity({{V}_{\max }})}{\omega }$ ,
Now, maximum velocity $\left( {{V}_{\max }} \right)=A\omega$.
${{V}_{\max }}=0.248\times \dfrac{2\times 3.14}{1}=1.56m/s$.

So, the correct answer is “Option A”.

Note:
In the formula ${{\omega }^{2}}A=\left( \dfrac{2\pi }{T} \right)A=g$, $\omega =2\pi \gamma$ and we know that $\gamma =\dfrac{1}{T}$ so, $\omega =\dfrac{2\pi }{T}$ , in this way we are getting the above formula. In this formula A is the amplitude, T is the time period and ‘g’ is the acceleration due to gravity.