Question

A block of mass $M$ is pulled along a horizontal frictionless surface by rope of mass $m$ by applying a force $P$ at one end of the rope. The force which the rope exerts on the block is
(A) $\dfrac{{PM}}{{M - m}}$
(B) $\dfrac{{MP}}{{M + m}}$
(C) $\dfrac{{pm}}{{M + m}}$
(D) $P$

Answer 1

Consider Newton's third law of motion; recall the concept of action-reaction pair.There is a reaction force that is present when we apply a force on the block.The whole system will move with a single acceleration.We can use the free body diagram of the rope.

Complete step by step answer:
Consider the Newton’s second law of motion,
$force(f) = mass \times acceleration(a)$
Force ($P$) is applied at the end of the rope, the other end is attached with the block.
And mention that there is a frictionless surface, so we can neglect the frictional force contribution.
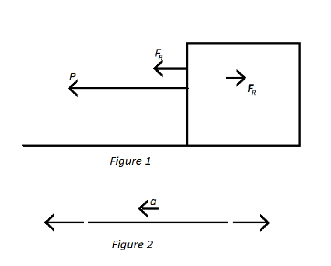
The figure$1$has shown the block mass $M$ is attached with a rope having mass $m$ pulled by the rope with a force$P$.
There is a force ${F_B}$is acting on the block at the end of rope, there is also a reactive force coming from the block is
${F_R} = \dfrac{{(M + m)P}}{{M + m}} - \dfrac{{mP}}{{M + m}} = \dfrac{{MP}}{{M + m}}$
${F_R} = {F_B}$
The whole system has same acceleration and denoted by $a$
Acceleration is equal to the total applied force divided by total mass.
Total mass $= m + M$
Applied force $= P$
Acceleration $a = \dfrac{P}{{M + m}}$
Consider figure$2$, the free body diagram of rope is shown.
From this,
The reaction force is opposite to the applied force, so the difference is,
$P - {F_R} = mass \times acceleration$
Substitute the acceleration of rope and mass. Then,
$P - {F_R} = m \times \dfrac{P}{{M + m}}$
Rearrange the equation,
$P - {F_R} = \dfrac{{mP}}{{M + m}}$
${F_R} = P - \dfrac{{mP}}{{M + m}}$
${F_R} = \dfrac{{(M + m)P}}{{M + m}} - \dfrac{{mP}}{{M + m}} = \dfrac{{MP}}{{M + m}}$
From action-reaction pair, so that these reaction force from the box is equal to the force applied by the end of the rope, in equation,
${F_R} = {F_B}$
${F_B} = \dfrac{{MP}}{{M + m}}$
So the answer is (B) $\dfrac{{MP}}{{M + m}}$

Note: Always remember following points in order to solve such type of problems:
1)Action reaction is always paired.
2)Easy to solve this kind of problem with a free body diagram.
3)Any force can equate to product mass of mass and acceleration.