Question

A block of mass m is placed on another block of mass M, which itself is lying on a horizontal surface. The coefficient of friction between two blocks is u and that between the block of mass M and the horizontal surface is u. What is maximum horizontal force can be applied to the lower block so that the two blocks move without separation?
A. $(M + m({\mu _2} - {\mu _1})g$
B. $(M - m)({\mu _2} - {\mu _1})g$
C. $(M - m)({\mu _2} - \mu )g$
D. $(M + m)({\mu _2} - {\mu _1})g$

Answer 1

Concept of laws of motion and friction force. As the total force acts on the combined mass that is M+ m, So it gives it net acceleration but only the resistive force acting here will be the friction force that between mass M and the horizontal surface.

Complete step by step solution:

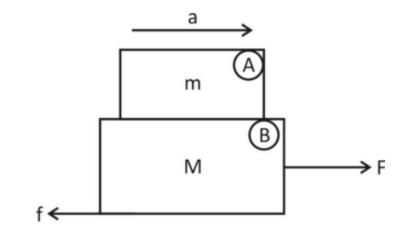
Let us consider two block, $A$and $B$as shown in figure with mass $M$
Now, according to the question the force applied $F$should be such that the upper block does not move
i.e Force applied , should be more than the limiting friction
Limiting friction for upper block, $A = {\mu _1}R$
Now, we know that $R = mg$
So,
Limiting friction $= {\mu _1}mg$
Now, for non slipping condition,
If $\leqslant {\mu _1}mg$
$ma = {\mu _1}mg$ (Maximum force $f = ma$for upper block)
$\Rightarrow a = {M_1}g$ ….. (i)
Where a is the net acceleration of the system.
$F - {\mu _2}R' = (M + m)a$ ….. (ii)
Where $R' = (M + m)g$
So, equation (ii) becomes
$F - {\mu _2}(M + m)g = (M + m)a$
$F = (M + m)a + (M + m){\mu _2}g$
$F = (M + m)(a + {\mu _2}g)$
From (i), $a = {M_1}g$
So, $F = (M + m)({\mu _1}g + {\mu _2}g)$
$F = (M + m)({\mu _1} + {\mu _2})$g

Hence the correct answer is D.

Note: Here we have to solve using free body diagram for upper block from where it comes $f = {\mu _1}mg$. Also for non-slipping condition, maximum friction acting is limiting friction which is maximum value of static friction after which the body starts moving.