Question

A block of mass $m$ is placed on an inclined plane. With what acceleration $A$ towards the right should the system move on a horizontal surface so that $m$ does not slide on the surface of the inclined plane? Also, calculate the force supplied by the wedge on the block. Assume all surfaces are smooth.

Answer 1

-Divide the forces acting on the block into their vertical and horizontal components at the angle between the inclined plane and horizontal plane.
-Express the force in terms of the acceleration (both linear and gravitational).
-The resultant force for the horizontal direction should be zero for the condition of the non-sliding of the block.
-Calculate the linear acceleration and then the force using this condition.

Formula used:
The weight of the block $W = mg$ $g$ is the gravitational acceleration,
The force acting on the block due to the acceleration $A$, $F = mA$
The resultant force for the forces acting horizontally,$mA\cos \theta - mg\sin \theta = 0$ [ not to make the block slide]
$mA\cos \theta$ is the horizontal component of the force $F( = mA)$
$mg\sin \theta$ is the horizontal component of the weight of the block $W( = mg)$

Complete step by step answer:
An inclined plane is kept in a block of mass $m$. The block is about to slide with an acceleration $A$. The forces acting on the block are (i) The force due to its weight $W = mg$
(ii) The force due to the acceleration $A$, $F = mA$
(iii) the normal force by the inclined plane $n$.

Now if we modify the above diagram by showing the components of the applied forces it will be as follow,

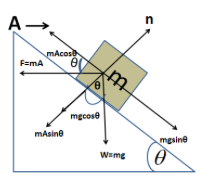
$mA\cos \theta$is the horizontal component and $mA\sin \theta$ is the vertical component of the force $F( = mA)$.
$mg\sin \theta$ is the horizontal component and $mg\cos \theta$ is the vertical component of the weight of the block $W( = mg)$.
The resultant force for the forces acting horizontally, $mA\cos \theta - mg\sin \theta$.
The resultant force for the horizontal direction should be zero for the condition of the non-sliding of the block.
Hence, $mA\cos \theta - mg\sin \theta = 0$
$\Rightarrow mA\cos \theta = mg\sin \theta$
$\Rightarrow A = \dfrac{{mg\sin \theta }}{{m\cos \theta }}$
$\Rightarrow A = \dfrac{{g\sin \theta }}{{\cos \theta }}$
Using the formula $\dfrac{{\sin \theta }}{{\cos \theta }} = \tan \theta$and we get,
$\Rightarrow A = g\tan \theta$
So, the acceleration $A$ towards the right should be $\Rightarrow A = g\tan \theta$, so that the block does not slide.
The force supply by the wedge of the block due to the acceleration $A$, $F = mA$
$\therefore F = mg\tan \theta$.

Note: The horizontal component of the force due to acceleration $A$ $mA\cos \theta$ is acting towards the left due to the block’s motion is towards the right. The force acting oppositely to stop the block. Hence the block would not slide if the Resultant force of the horizontal force components becomes zero.