Question

A block of mass $m$ is placed on a smooth wedge of inclination $\theta$. The whole system is accelerated horizontally so that block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude
A. $mg$
B. $mg\cos \theta$
C. $mg/\cos \theta$
D. $mg\tan \theta$

Answer 1

We can use the expression for Newton’s second law of motion. This formula gives the relation between the net force acting on the object, mass of the object and acceleration of the object. First we should draw the free body diagram of the block on the inclined wedge. Then first apply Newton’s second law of motion to the block in the horizontal direction and then in the vertical direction.

Formula used:
The expression for Newton’s second law of motion is given by
${F_{net}} = ma$ …… (1)
Here, ${F_{net}}$ is the net force acting on the object, $m$ is mass of the object and $a$ is acceleration of the object.

Complete step by step answer:
We have given that the mass of the block is $m$and it is placed on a smooth wedge at an angle of inclination $\theta$ with the horizontal. We have also given that the system of the wedge and block has given a horizontal acceleration. We are asked to determine the force exerted by the wedge on the block. Let $a$ be the horizontal acceleration given to the system of block and wedge. The force exerted by the surface of the wedge on the block is the normal force as the block is in contact with the wedge surface. Let us first draw the free body diagram of the block.

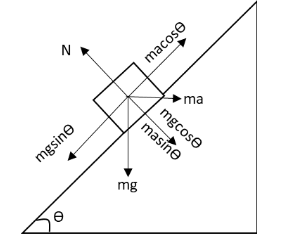
In the above free body diagram, $mg$ is the weight of the block in the downward direction and $N$ is the normal force exerted by the wedge on the block. The components of the weight of the block and force due to horizontal acceleration are shown in the above free body diagram.

Let us first apply Newton’s second law of motion to the block in the horizontal direction.
$mg\sin \theta = ma\cos \theta$
$\Rightarrow a = g\dfrac{{\sin \theta }}{{\cos \theta }}$
$\Rightarrow a = g\tan \theta$
Let us now apply Newton’s second law of motion to the block in the vertical direction.
$N = mg\cos \theta + ma\sin \theta$
Substitute $g\tan \theta$ for $a$ in the above equation.
$N = mg\cos \theta + ma\sin \theta$
$\Rightarrow N = mg\cos \theta + m\left( {g\tan \theta } \right)\sin \theta$
$\Rightarrow N = mg\cos \theta + m\left( {g\dfrac{{\sin \theta }}{{\cos \theta }}} \right)\sin \theta$
$\Rightarrow N = mg\cos \theta + mg\dfrac{{{{\sin }^2}\theta }}{{\cos \theta }}$
$\Rightarrow N = mg\left( {\cos \theta + \dfrac{{{{\sin }^2}\theta }}{{\cos \theta }}} \right)$
$\Rightarrow N = mg\left( {\dfrac{{{{\cos }^2}\theta + {{\sin }^2}\theta }}{{\cos \theta }}} \right)$
$\Rightarrow N = mg\left( {\dfrac{1}{{\cos \theta }}} \right)$
$\therefore N = \dfrac{{mg}}{{\cos \theta }}$
Therefore, the force exerted by the wedge on the block is $\dfrac{{mg}}{{\cos \theta }}$.

Hence, the correct option is C.

Note: The students should be careful while applying Newton’s second law of motion to the block. In the free body diagram of the block, we have considered the direction perpendicular to the inclined surface of the wedge as positive Y-axis and the direction perpendicular to this Y-axis in the right hand direction as the positive X-axis. The normal horizontal and vertical directions of the X and Y-axis are not considered in the free body diagram.