Question

A block of mass m is placed at rest on an incline plane of inclination $\theta$ to the horizontal. If the coefficient of friction between the block and the plane is $\mu$, then the total force exerted by the inclined plane on the block is:
A. $mg$
B. $\mu mg\cos \theta$
C. $mg\sin \theta$
D. $\mu mg\tan \theta$

Answer 1

The question talks about moving an object (block) on an incline which is sliding and at angle of $\theta$ to the X direction, with the block exerting a weight on the plane and the plane dashing its weight (reaction) to the block. Use the resolution of forces to solve this question

Complete step by step answer:
We are given that a block of mass m is placed at rest on an inclined plane of inclination $\theta$ to the horizontal and the coefficient of friction between the block and the plane is $\mu$
We have to calculate the total force exerted by the inclined plane on the block.

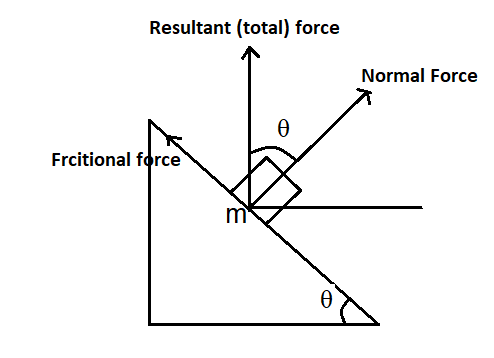
When two objects slide over each other, the object above exerts a frictional force on the object below, and the object below also exerts equal amount of force known as the normal reaction.
Force acting to the horizontal is the normal force due to inclined plane on the block which is $mg\cos \theta$
Force acting to the vertical is the frictional force which is $mg\sin \theta$
Then the total force is the sum of normal force and frictional force and normal force and frictional force are perpendicular to each other.
$Forc{e_{total}} = Forc{e_{normal}} + Forc{e_{frictional}} \\\ \implies Forc{e_{total}} = mg\sqrt {{{\sin }^2}\theta + {{\cos }^2}\theta } \\\ \implies Forc{e_{total}} = mg\left( {\therefore {{\sin }^2}\theta + {{\cos }^2}\theta = 1} \right) \\\$
Therefore, the correct option is Option A, $mg$

So, the correct answer is “Option A”.

Additional Information:
Total force exerted is the sum of frictional force and the normal force. Frictional force is $mg\sin \theta$ and normal force is $mg\cos \theta$
Normal force and frictional force are perpendicular to each therefore the angle between them is 90 degrees
$F = mg\sin \theta + mg\cos \theta \\\ \theta = {90^ \circ } \\\ \implies F = mg\sin {90^ \circ } + mg\cos {90^ \circ } \\\ \sin {90^ \circ } = 1,\cos {90^ \circ } = 0 \\\ \implies F = mg\left( 1 \right) + mg\left( 0 \right) = mg \\\$
The total force exerted is $mg$.

Note:
We can also see that when taken for example, a book is placed on a table or desk. There is always a force exerted from the book down wards (weight) and also a reaction from the table or desk. The forces counter balance themselves.