Question

A block of mass $m$ is kept on a platform which starts from rest with a constant acceleration $\dfrac{g}{2}$ upwards, as shown in the figure. Work done by normal reaction on block in time $t$ is _____?

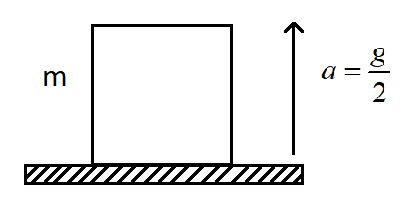
(A) 0
(B) $\dfrac{{3m{g^2}{t^2}}}{8}$
(C) $- \dfrac{{m{g^2}{t^2}}}{8}$
(D) $\dfrac{{m{g^2}{t^2}}}{8}$

Answer 1

Hint : We need to first draw the free body diagram of the mass $m$ and from here we can find the value of the normal reaction force that is acting on the mass. Now using the equation of motion we can find the displacement of the body. Since the force and displacement will be in the same direction, so the work done will be the product of the force and displacement.

Formula Used: In this solution we will be using the following formula,
$\Rightarrow F = ma$
where $F$ is the net force acting on the body
$m$ is the mass of the body and $a$ is the acceleration of the body.
$\Rightarrow S = ut + \dfrac{1}{2}a{t^2}$
where $S$ is the displacement, $u$ is the initial velocity and $t$ is the time.

Complete step by step answer
To solve this problem, we need to first draw the free body diagram of the mass m. So we have,

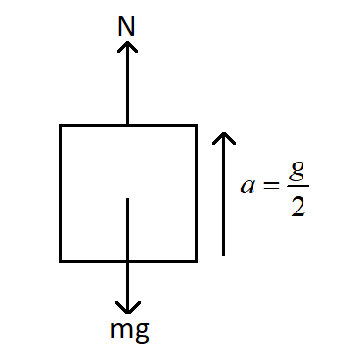
From the diagram we can see that the normal reaction force is acting on the body in an upward direction and the weight of the body is acting in the downward direction. The net acceleration is produced in the body in the upward direction. Hence we can write,
$\Rightarrow N - mg = ma$
In the question we are given $a = \dfrac{g}{2}$ . Therefore substituting we get,
$\Rightarrow N - mg = m\dfrac{g}{2}$
Keeping only the $N$ in the LHS we get,
$\Rightarrow N = \dfrac{{mg}}{2} + mg$
Therefore we have,
$\Rightarrow N = \dfrac{{3mg}}{2}$
This is the normal reaction force acting on the body. Now, to find the work done by this force we need to find the displacement of the body. The body is initially at rest so, $u = 0$ and the time is given in the question as $t$ . So we can use the equation of motion, $S = ut + \dfrac{1}{2}a{t^2}$ . Substituting we get,
$\Rightarrow S = 0 + \dfrac{1}{2} \times \dfrac{g}{2}{t^2}$
Hence we get the displacement as,
$\Rightarrow S = \dfrac{{g{t^2}}}{4}$
The work done by a force is given by the formula, $W = FS\cos \theta$
Now since the normal reaction force and the displacement are in the same direction so $\theta$ is zero. Hence we have, $W = FS$
Substituting the $N = \dfrac{{3mg}}{2}$ in place of $F$ and $S = \dfrac{{g{t^2}}}{4}$ in place of the displacement we get,
$\Rightarrow W = \dfrac{{3mg}}{2} \times \dfrac{{g{t^2}}}{4}$
On calculating we get,
$\Rightarrow W = \dfrac{{3m{g^2}{t^2}}}{8}$
So we get the work done as, $\dfrac{{3m{g^2}{t^2}}}{8}$ . So the correct answer is option (B).

Note
A free body diagram is a graphical illustration of a diagram depicting the forces that are acting on the body and the resulting momentum of the body. The forces are depicted using straight lines pointing towards the direction of the force.