Question
Question: A block of mass \(m\) is connected to another block of mass \(M\) by a massless spring of spring con...
A block of mass m is connected to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.
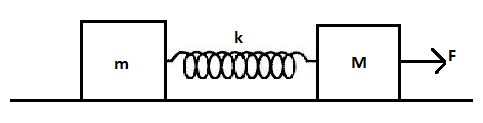
Solution
First calculate the acceleration of the system using newton’s second law of motion. Then calculate the pseudo force acting on each of the blocks due to the Force F. Taking spring forces into account, calculate the net work done by the system and equate it to 0 (as it will be zero). On solving, you will get the answer for maximum extension of the spring.
Formula Used:
Force, F=ma where, m is the mass of the body, a is the acceleration of the body
Work Done WD=ΔKE=f×s where, KE is the kinetic energy of the system, f is net force acting on the body and s is displacement of the body.
Complete step by step solution:
The first block has a mass m and the second block has a mass M . Second block is pulled with a force F and as a result, the entire system will experience the force.
Therefore, the acceleration of the system will be, asys=msysFsys where F is the force experienced by the system and m is the mass of the system.
⇒asys=M+mF (total mass of system will be the addition of masses of both the blocks)
This is the acceleration each of the block will have in the direction of force F
Now, these blocks will develop a pseudo force, acting in the opposite direction of force F to balance this force.
The magnitude of this pseudo force for block of mass m , Fpseudo=m×asys=M+mFm
The magnitude of this pseudo force for block of mass M , Fpseudo=M×asys=M+mFM
The block with mass m experiences only this pseudo force, so net force acting on it =M+mmF
(this net force is in a direction opposite to direction of F )
The block with mass M experiences this pseudo force as well as the force F , so net force acting on it =F−M+mMF (since F is greater than the pseudo force) (this net force is in direction of F )
Now due these net forces acting on the blocks, they will move in their respective directions.
Block of mass m will move in direction of pseudo force (left). Let the distance covered by it till it stops be x1
Block of mass M will move in direction of F (right). Let the distance covered by it till it stops be x2
Therefore, the total extension in the spring will be (x1+x2)
This spring will also exert a force, called spring force and will oppose the motion of the blocks. After some time, due to this force, the blocks will stop moving. At this point the spring force becomes equal to the net forces acting on the blocks that we calculated above.
Now, according to work-energy theorem, net work done of a body, WDnet=ΔKE=21mvfinal2−21mvinitial2 where m is the mass of the system and vinitial,vfinal are the initial and final velocities of the system.
For this system, the initial velocity is zero (the blocks were initially at rest)
Also, the blocks are finally at rest too, as explained above so final velocity is also zero.
This means ΔKE=0 or, WDnet=0
Now we also know that WDnet=f×s where f is the net force acting on the body and s is the displacement.
Applying this formula to both the blocks and the spring, we get
WDnet=(M+mmF×x1)+((F−M+mMF)×x2)−21k(x1+x2)2 where, k is the spring constant.
(minus sign indicates that the direction of force and displacement are opposite)
On further solving this, we get WDnet=(M+mmF×x1)+(M+mmF×x2)−21k(x1+x2)2
Also, we have derived that WDnet=0
Combining these two equations, (M+mmF×x1)+(M+mmF×x2)−21k(x1+x2)2=0
⇒(M+mmF)(x1+x2)−21k(x1+x2)2=0
⇒(x1+x2)[(M+mmF)−21k(x1+x2)]=0
Now, this equation has two possibilities, one says (x1+x2)=0
This means that one of the blocks has negative mass or both of them have no mass. This makes no sense. This possibility will be rejected.
For the second possibility, we have (M+mmF)−21k(x1+x2)=0
Or, (M+mmF)=21k(x1+x2)
⇒k(M+m)2mF=(x1+x2)
This will be the maximum extension in the spring. Hence, this is the final answer.
Note: Whenever a force is applied to a body, a pseudo force is also generated to balance the force applied to it, according to the laws of physics. It is generated in a direction opposite to the direction in which the force is physically applied. Same is the case with a spring. When it is extended, it generates a force in the opposite direction to oppose the extension of spring. This force is called the spring force.
