Question

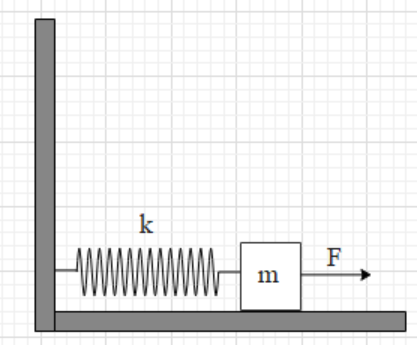
A block of mass m is connected to a spring of force constant k. Initially, the block is at rest and the spring has a natural length. A constant force F is applied horizontally towards the right. The maximum speed of the block will be (there is no friction between the block and the surface)

$\text{A}\text{. }\dfrac{F}{\sqrt{2mK}}$
$\text{B}\text{. }\dfrac{F}{\sqrt{mK}}$
$\text{C}\text{. }\dfrac{\sqrt{2}F}{\sqrt{mK}}$
$\text{D}\text{. }\dfrac{2F}{\sqrt{mK}}$

Answer 1

Analyse the given case. Initially, the net force on the block is F, and the acceleration of the block is maximum. As the block moves, the spring force will increase in the opposite direction and the net force will begin to decrease. When the net force is zero, the block will have a maximum speed, i.e. when kx=F. Then, calculate the work by the spring and the force F and equate it to the change in kinetic energy of the block.

Formula Used:
${{F}_{s}}=kx$
${{W}_{s}}=-\dfrac{1}{2}k{{x}^{2}}$
W=Fx

Complete step-by-step solution:
Let us analyze the given case. It is given that initially, the spring is in its natural length. When the force F is applied on the block (as shown) the block will accelerate in the right direction (according to the second’s law of motion).
However, when the block moves towards the right, it is stretched. Hence, the spring will apply a pulling force on the block, that is towards the left. The value of spring force is given as ${{F}_{s}}=kx$, where x is the extension or compression in the spring.
The net force on the block is $F-{{F}_{s}}\Rightarrow F-kx$
As the block moves further, the value of x increases, and thus the spring force increases. As a result, the net force on the block on the block becomes lesser and lesser.
Since the net force on the block is decreasing, the acceleration of the block is decreasing. Therefore, when ${{F}_{s}}=F\Rightarrow kx=F$, the acceleration of the block will be zero.
i.e. when $x=\dfrac{F}{k}$
Then, as the block moves further, the spring force is greater than F. Therefore, the net force shifts towards left, and thus the block will accelerate towards left. Since the block starts to accelerate in the opposite direction, the velocity of the block will begin to decrease.
This means that the block has a maximum speed (v) at $x=\dfrac{F}{k}$.
Let us use the work-energy theorem, which says that the total work done is equal to the change in kinetic energy of the body.
Work done by spring force is ${{W}_{s}}=-\dfrac{1}{2}k{{x}^{2}}$ .
And the work done by the force F is W=Fx.
Since the block was at rest initially, the change in its kinetic energy is $\Delta K=\dfrac{1}{2}m{{v}^{2}}$
And ${{W}_{s}}+W=\Delta K$.
$\Rightarrow -\dfrac{1}{2}k{{x}^{2}}+Fx=\dfrac{1}{2}m{{v}^{2}}$.
Substitute the value of $x=\dfrac{F}{k}$.
$\Rightarrow -\dfrac{1}{2}k{{\left( \dfrac{F}{k} \right)}^{2}}+F\left( \dfrac{F}{k} \right)=\dfrac{1}{2}m{{v}^{2}}$
$\Rightarrow -{{\dfrac{F}{2k}}^{2}}+\dfrac{{{F}^{2}}}{k}=\dfrac{1}{2}m{{v}^{2}}$
$\Rightarrow \dfrac{{{F}^{2}}}{2k}=\dfrac{1}{2}m{{v}^{2}}$
$\Rightarrow {{v}^{2}}=\dfrac{{{F}^{2}}}{mk}$
$\Rightarrow v=\dfrac{F}{\sqrt{mk}}$.
Therefore, the maximum speed of the block is equal to $\dfrac{F}{\sqrt{mk}}$.
Hence, the correct option is B.

Note: The sum of the potential energy of the spring and the kinetic energy of the body is called the mechanical energy of the spring block system.
The potential energy of the spring is given as $U=\dfrac{1}{2}k{{x}^{2}}$.
The kinetic energy of the body is $K=\dfrac{1}{2}m{{v}^{2}}$
The mechanical energy of the system is also to the work done by the external force, i.e. W=Fx.
Therefore, W = K +U.
$Fx=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}k{{x}^{2}}$.
Here can substitute the value $x=\dfrac{F}{k}$ and find the value of v.