Question
Question: A block of mass \[m\] is connected to a spring of force constant \[k\]. Initially the block is at re...
A block of mass m is connected to a spring of force constant k. Initially the block is at rest and the spring has natural length. A constant force F is applied horizontally towards the right. The maximum speed of the block will be (there is no friction between block and the surface)
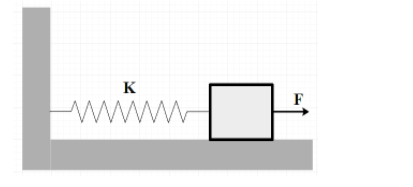
Solution
We will use the expression given for force on a spring. This force is directly proportional to the displacement of the body. Then we will apply the law of conservation of energy which gives the work done due to the force equal to the total energy of the body. Total energy of the body comprises the kinetic energy of the mass and the energy due to the spring.
Complete step by step answer:
We will redraw the diagram for better understanding of the situation.
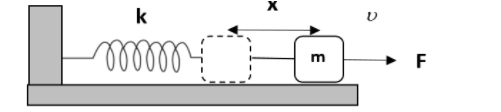
Now, the distance moved by the force will be equal to kF=xfrom the restoring force equation.
We will find the work done by the applied force, which is given as,
W=F.x
Where, Fis force applied and x is the distance moved by the object. But we found the expression for distance moved by using the formula for restoring force. Hence, work done by the force will be,
W=F×(kF)=kF2
Now, the total energy of the body will be the sum of kinetic energy due to the movement and potential energy due to the spring which is given as,
Et=21mv2+21kx2
This energy will be equal to the work done by the force. We will equate the two expressions and then find the expression for velocity of the body.
