Question
Question: A block of mass m is attached to a massless spring of force constant k. The block is placed over a r...
A block of mass m is attached to a massless spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=43 . The minimum value of M required to move the block up the plane is (Neglect mass of string and pulley and friction in pulley):
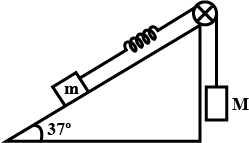
(a)53m(b)54m(c)2m(d)23m
Solution
We will first write the force equation on the small block (m) to get the required length of spring that must stretch down in order to just move the block up the inclined surface. We will then apply the Work Energy theorem for conservation of energy on the small block (m) to get the required solution.
Complete answer:
Let the mass M descend x meters to just move the block up on the incline. Then, writing the force equation on block M in the vertical direction, we get:
⇒Mg=kx
Where,
kx is the spring force.
Now, for the small block (m) , force acting on it along the inclined surface are:
kx : force due to the spring, up the incline
mgsinθ: down the incline
μmgcosθ: down the incline
Thus, the net force on the block can be written as:
⇒kx=mgsinθ+μmgcosθ⇒kx=mg(sinθ+μcosθ)
Here, it has been given to us:
⇒g=10ms−2⇒μ=33⇒sinθ=53⇒cosθ=54
Putting these values in the above equation, we get:
⇒kx=10m(53+43×54)⇒kx=10m(56)⇒kx=12m
Now, applying the Work-Energy theorem:
⇒Wgravity+Wspring+Wfriction=△K.E.
Here,
⇒Wgravity=Mgx⇒Wspring=21kx2⇒Wfriction=0⇒△K.E.=0
Putting these values in above equation, we get:
⇒Mgx+(−21kx2)+0=0⇒M=20kx
Using the value of kx calculated above, we get the value of M as:
⇒M=2012m⇒M=53m
Hence, the minimum value of M to move the block up the incline should be 53m
Hence, option (a) is the correct option.
Note:
It should be noted that, in the problem the statement was “just to move the block up”. This means that the block did not gain any velocity in the process and that it has been moved very slowly. This is the reason why, in the Work-Energy equation we wrote the value of change in kinetic energy of the block as zero and not something finite.
