Question
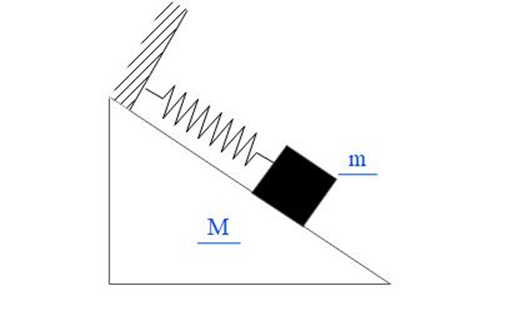
Question: A block of mass m is attached to a fixed position on a smooth wedge of mass M. The block oscillates ...
A block of mass m is attached to a fixed position on a smooth wedge of mass M. The block oscillates along the incline with amplitude a and angular frequency ω. Wedge is located on a rough surface of friction μ. Find the friction acting on the wedge if it always remains at rest.
a)μ(M+m)gb)21mω2Asin(ωt+ϕ)c)μ(M+m)ω2Asin(ωt+ϕ)d)none
Solution
When the wedge is at rest, the net frictional force can be calculated by finding out the horizontal component of net force acting on the block of mass m. Given the angle of the wedge, we can divide the force acting into horizontal and vertical components.
Formula used:
x=Asin(ωt+ϕ)F=ma=mω2xF=mω2Asin(ωt+ϕ)
Complete step-by-step answer:
The net force on the mass m in the vertical component and horizontal component will be Fsin600,Fcos600respectively. The displacement made by the mass m due to the spring system will be, x=Asin(ωt+ϕ)where A,ω,ϕare amplitude, angular frequency and phase angle respectively.
Now, the horizontal component of the force acting on mass m will be equal to the frictional force acting on the wedge as the net horizontal forces acting on the system must be equal. Therefore, we get,
Fcos600=mω2xcos600f=Fcos600=21mω2Asin(ωt+ϕ)
Therefore, the frictional force acting on the mass is option b.
So, the correct answer is “Option b”.
Additional Information: System in which both masses and springs are present will have several degrees of freedom. It can be described using two generalized coordinates. The frequency of the system when no external force is acting is called eigen frequency or natural frequency. The gravitational force will not affect the period of oscillation of the mass on a spring. Gravitational force will affect the equilibrium extension. The force exerted by a compressed or stretched spring upon any object that is attached to it.
Note: The time period depends on the mass and spring constant of the spring. It is directly proportional to square root of mass and inversely proportional to square root of spring constant. The net forces on the overall system are conserved always. We can use this way to find out the normal force or frictional force.
