Question

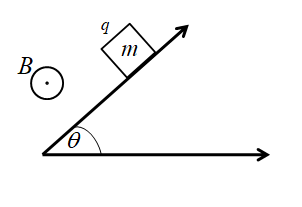
A block of mass $m$ and charge $q$ is released on a long smooth inclined plane magnetic field $B$ is constant, uniform, horizontal, and parallel to the surface as shown. Find the time from the start when the block loses contact with the surface.

$(A)\dfrac{{m\cos \theta }}{{qB}}$
$\left( B \right)none$
$(C)\dfrac{{msec\theta }}{{qB}}$
$(D)\dfrac{{m\cot \theta }}{{qB}}$

Answer 1

A free body diagram has to be drawn for the block showing the forces act on it. From the diagram, the force is found in terms of the mass of the block. Another force exists here due to the charge on a magnetic field. By equating these forces for the given condition the velocity of the block can be calculated. After getting the velocity the required time can also be found from the equation of motion of the block.

Formula used:
${F_1} = mg\cos \theta$
$mg$ is the weight of the block and $mg\cos \theta$ is the cosine component of $mg$
The force ${F_1}$ is acting equal and opposite to the cosine component of the weight of the block.
The force occurs due to the magnetic field,
${F_2} = qvB$
$B$ is the magnetic field and charge $q$
The velocity at time $t$
$v = g\sin \theta .t$

Complete answer:
The given diagram is,

The diagram has to be modified to show the forces acting on it and also on the system.

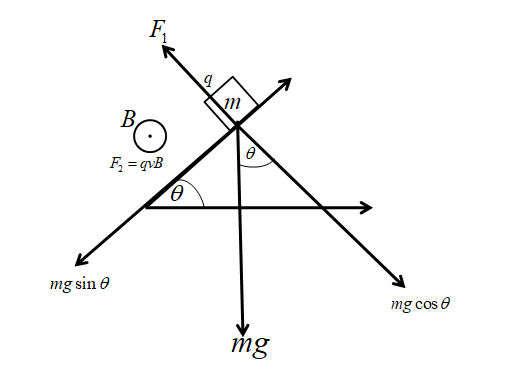
The weight of the block $mg$ is acting normally downwards to the block and it is divided into two components $mg\cos \theta$ and $mg\sin \theta$at the angle of $\theta$ (angle of inclination).
The force ${F_1}$ is acting equal and opposite to the cosine component of the weight of the block.
So, ${F_1} = mg\cos \theta$
And due to the magnetic field $B$ and charge $q$ the force occurs, ${F_2} = qvB$,
$v$ is the velocity.
These two forces are equal when the block start leaving the incline plane having the effect of the magnetic field,
So, ${F_1} = {F_2}$
$\Rightarrow qvB = mg\cos \theta$
$\Rightarrow v = \dfrac{{mg\cos \theta }}{{qB}}$
Now the velocity of the block at time $t$ ,
$v = g\sin \theta .t$
$\Rightarrow t = \dfrac{v}{{g\sin \theta }}$
put the value of $v$ we get,
$\Rightarrow t = \dfrac{{\dfrac{{mg\cos \theta }}{{qB}}}}{{g\sin \theta }}$
$\Rightarrow t = \dfrac{{m\cos \theta }}{{qB\sin \theta }}$
$\Rightarrow t = \dfrac{{m\cot \theta }}{{qB}}$
So, the time from start when block loses contact with the surface $\Rightarrow t = \dfrac{{m\cot \theta }}{{qB}}$
Hence, the right answer is in option (D).

Note:
The magnitude of the force on a magnetic field having a charge $q$ is $F = qvB\sin \theta$ where $\theta$ is the angle $< {\text{ }}180$ degrees between the velocity and the magnetic field. This shows that the magnetic force on a stationary charge or a charge moving parallel to the magnetic field is zero. if the direction of the velocity is normal to the magnetic field the force will be$F = qvB$. The direction of the force is given by the right hand rule.