Question

A block of mass $M = 9kg$ is moving with uniform velocity of $2m/s$ on a rough horizontal surface under the action of constant force $F$. The force acts at an angle $37^\circ$ to the horizontal. Find work done by the force $F$ during an interval of $4s$ of motion.

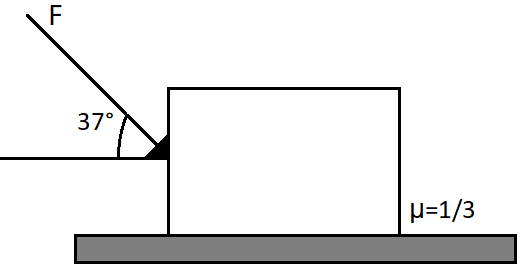
(A) $400J$
(B) $300J$
(C) $320J$
(D) $100J$

Answer 1

Hint
We need to draw the free body diagram of the block first. From there using the equation of motion of the block we need to calculate the force $F$. The displacement will be the product of the time and velocity as the velocity is constant. The work done can be then calculated by the dot product of the force and the displacement.
In this solution we will be using the following formula,
$\Rightarrow W = \vec F \cdot \vec S = FS\cos \theta$
where $F$ is the force, $S$ is the displacement and $\theta$ is the angle between the force and displacement.

Complete step by step answer
To solve this problem we need to first draw the free body diagram of the block taking into consideration all the forces acting on the block.

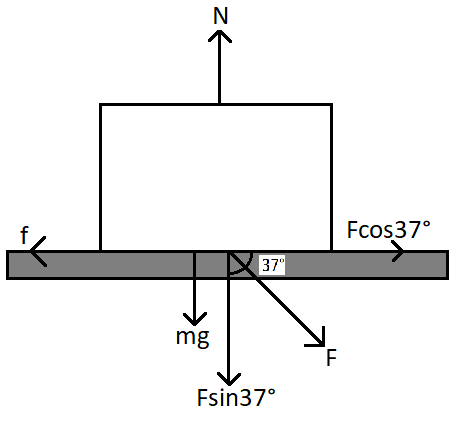
Now since there is no acceleration on the block in the horizontal or the vertical direction, the sum of the forces in the horizontal direction and the vertical direction balance each other.
Now in the vertical direction, we can see there is the sine component of the force $F$ in the downward direction and the weight of the body $mg$ acting in the downward direction. The normal reaction force on the body due to the surface is in the upward direction.
So we can set the equation as,
$\Rightarrow N = F\sin 37^\circ + mg$
Now in the question we are given $m = 9kg$ and the acceleration due to gravity is taken approximately $g = 10m/{s^2}$. The value of $\sin 37^\circ$ can be approximately taken as, $\Rightarrow \sin 37^\circ = \dfrac{3}{5}$
So substituting these values in the equation we get,
$\Rightarrow N = F\dfrac{3}{5} + 9 \times 10$
Therefore the normal reaction force on the body is equal to
$\Rightarrow N = \dfrac{{3F}}{5} + 90$
Now in the horizontal direction, from the diagram, we can see that the cosine component of the applied force is balanced by the force of friction. The force of friction is denoted here by $f$ and it can be calculated by $f = \mu N$ where $\mu$ is the coefficient of friction between the 2 surfaces. In the diagram in the question, we are given the coefficient of friction as, $\mu = \dfrac{1}{3}$ and the normal reaction force is calculated above as, $N = \dfrac{{3F}}{5} + 90$. Substituting these values we get the force of friction as,
$\Rightarrow f = \dfrac{1}{3}\left( {\dfrac{{3F}}{5} + 90} \right)$
On opening the bracket we get,
$\Rightarrow f = \dfrac{F}{5} + 30$
Therefore in the horizontal direction we can write the equation of motion of the body as,
$\Rightarrow f = F\cos 37^\circ$
Substituting values,
$\Rightarrow \dfrac{F}{5} + 30 = F\cos 37^\circ$
Now the value of $\cos 37^\circ$ is approximately, $\cos 37^\circ = \dfrac{4}{5}$
Hence we get in the equation,
$\Rightarrow \dfrac{F}{5} + 30 = \dfrac{{4F}}{5}$
On taking $\dfrac{F}{5}$ to the other side we have,
$\Rightarrow \dfrac{{4F}}{5} - \dfrac{F}{5} = 30$
On doing the subtraction we get,
$\Rightarrow \dfrac{{\left( {4 - 1} \right)F}}{5} = 30$
We take all the terms except $F$ from LHS to RHS and get the value of $F$ as,
$\Rightarrow F = \dfrac{{30 \times 5}}{3} = 50N$
This is the force exerted on the body. Now the displacement of the body is given by the product of velocity and time since the acceleration is zero. Therefore, we have
$\Rightarrow S = v \times t$
According to the problem, the velocity is $v = 2m/s$ and time is $t = 4s$. On doing the product we get
$\Rightarrow S = 2 \times 4 = 8m$
Now the work done on the body is given by the formula,
$\Rightarrow W = \vec F \cdot \vec S = FS\cos \theta$
Where we have $F = 50N$, $S = 8m$ and the angle between the force and displacement as, $\theta = 37^\circ$
Hence substituting we get,
$\Rightarrow W = 50 \times 8 \times \cos 37^\circ$
Since $\cos 37^\circ = \dfrac{4}{5}$,
$\Rightarrow W = 400 \times \dfrac{4}{5}$
Cancelling we get, $W = 80 \times 4 = 320J$.
So the work done by the force is $320J$. So the correct answer is option (C).

Note
Work is said to be done by the force when there is a displacement of the body in the direction of the applied force. When the force acts on the body in the perpendicular direction to the displacement of the body, then no work is said to be done.