Question

A block of mass $m = 4kg$ is placed over a rough inclined plane as shown in Fig. The coefficient of friction between the block and the plane is $\mu = 0.5$. A force $F = 10N$ is applied on the block at an angle of ${30^ \circ }$. Find the contact force between the block and the plane.

A) $10.5\sqrt 5 N$
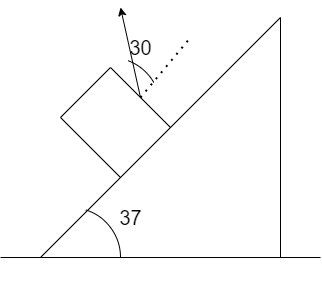
B) $13.5\sqrt 5 N$
C) $12.5\sqrt 5 N$
D) $10\sqrt 5 N$

Answer 1

A contact force is the force that can be exerted by one object on the other object if they are in contact or physically touching each other. Also when two objects or surfaces are in contact with each other, then friction force will be acting on two surfaces.

Complete step by step solution:
Step I: The resultant contact force acting on the body is the net normal force and the frictional force. It is written as
$R = \sqrt {{{(N)}^2} + {{(F)}^2}}$---(i)
Where N is the normal force and F is the frictional force.
The normal force is acting along the y-axis and the frictional force is acting on the x-axis.

Step II: Since the block is placed on an inclined plane, so the normal force will have two components- vertical and horizontal.
Normal force is given by
$N = mg$
Horizontal component is $mg\sin {37^ \circ }$
Vertical component is $mg\cos {37^ \circ }$

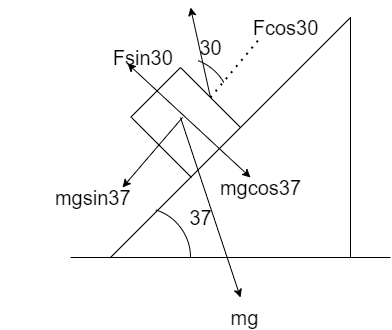
Step III: Also the friction force will be resolved into two components.
Horizontal component is $F\cos {30^ \circ }$
Vertical component is $F\sin {30^ \circ }$

Step IV: The mass on the inclined plane is balanced, so the net forces along the x axis will be zero. Hence,
${F_x} + mg\sin {37^ \circ } - F\cos {30^ \circ } = 0$
$\Rightarrow {F_x} + (4 \times 10 \times \dfrac{3}{5}) - (10 \times \dfrac{{\sqrt 3 }}{2}) = 0$
$\Rightarrow {F_x} = - 24 + 5\sqrt 3$
$\Rightarrow {F_x} = - 24 + 3.66$
$\Rightarrow {F_x} = - 15.34$

Step V: Similarly the effect of the forces on y-axis will also be zero. Therefore,
${F_y} = 0$
${N_y} + mg\cos {37^ \circ } - F\sin {30^ \circ } = 0$
$\Rightarrow {N_y} + (4 \times 10 \times \dfrac{4}{5}) - (10 \times \dfrac{1}{2}) = 0$
$\Rightarrow {N_y} = - 32 + 5$
$\Rightarrow {N_y} = - 27$

Step VI: Substituting the values in equation (i),
$R = \sqrt {{{( - 15.34)}^2} + {{( - 27)}^2}}$
The total contact force is
$R = 13.5\sqrt 5$

Hence Option (B) is the right answer.

Note: It is important to note that coefficient of friction is the relation between the force of friction and normal force of two surfaces. The value of coefficient is always less than $1$. This value shows that the value of normal force is equal and balanced by the frictional force.