Question

A block of mass m = 4 kg is attached to a spring of constant, k = 32 $Nm^{-1}$ by a rope that hangs over a pulley of mass M = 8kg. If the system starts from rest with the ideal spring unstretched, find the speed of the block after it falls 1 m. Treat the pulley as a uniform disc. (Assume there is no slipping between pulley and rope) (use g = 10$m/s^2$)

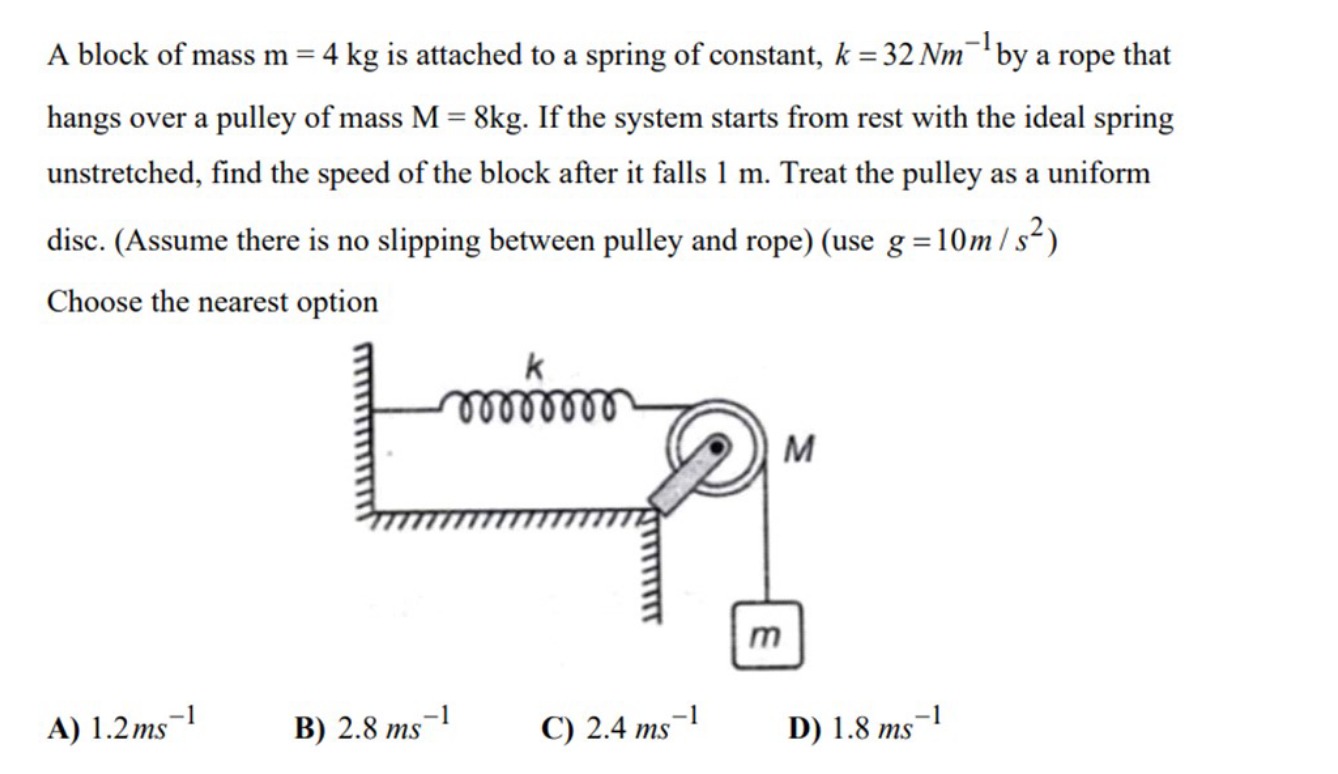
• A. 1.2$ms^{-1}$
• B. 2.8 $ms^{-1}$
• C. 2.4 $ms^{-1}$
• D. 1.8 $ms^{-1}$

Answer 1

Answer: (C)

2.4 $ms^{-1}$

Answer 2

Solution:

Using energy conservation, the drop in gravitational potential energy equals the sum of kinetic energies (of the block and the pulley) plus the potential energy stored in the spring. Thus,

$$mgh = \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2 + \frac{1}{2}kx^2$$

For a uniform disc pulley,

$$I = \frac{1}{2}MR^2 \quad \text{and} \quad \omega = \frac{v}{R}$$

so the rotational kinetic energy becomes:

$$\frac{1}{2}I\omega^2 = \frac{1}{2}\left(\frac{1}{2}MR^2\right)\left(\frac{v}{R}\right)^2 = \frac{1}{4}Mv^2.$$

Given:

• $m = 4\,\text{kg}$
• $M = 8\,\text{kg}$
• $k = 32\,\text{N/m}$
• $h = x = 1\,\text{m}$
• $g = 10\,\text{m/s}^2$

Substitute into the energy equation:

$$4 \times 10 \times 1 = \frac{1}{2}(4)v^2 + \frac{1}{4}(8)v^2 + \frac{1}{2}(32)(1)^2$$ $$40 = 2v^2 + 2v^2 + 16$$ $$40 = 4v^2 + 16 \quad \Longrightarrow \quad 4v^2 = 24 \quad \Longrightarrow \quad v^2 = 6$$ $$v = \sqrt{6} \approx 2.45\,\text{m/s}.$$

The nearest option is 2.4 m/s.