Question

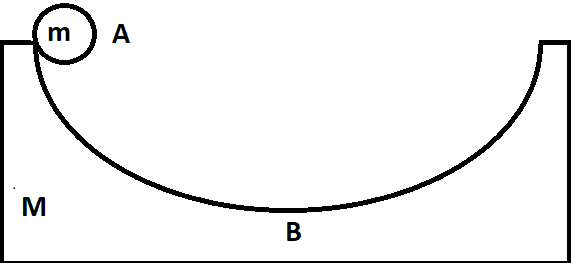
A block of mass $M=2kg$ with a semicircular track of radius R = 1.1m rests on a horizontal frictionless surface. A uniform cylinder of radius r = 10cm and mass m = 1.0kg is released from rest from the top point A. The cylinder slips on the semicircular frictionless track. The speed of the block when the cylinder reaches the bottom of the track at B is: $\left( {g = 10\,m\,{s^{ - 2}}} \right)$

A. $\sqrt {\dfrac{{10}}{3}\,} m\,{s^{ - 1}}$
B. $\sqrt {\dfrac{4}{3}\,} m\,{s^{ - 1}}$
C. $\sqrt {\dfrac{5}{2}\,} m\,{s^{ - 1}}$
D. $\sqrt {10\,} m\,{s^{ - 1}}$

Answer 1

When the cylinder starts to slip, the centre of mass (com) of the system also shifts. Besides this it also pushes the block in opposite direction due to normal force which it exerts due to contact with the block and as the system is on frictionless plane, it will generate velocity.

Complete step by step answer:
Let the cylinder slide down the track and reach the bottom of track at point B.
Assume the velocity of cylinder at point B (bottom of track) is v, (which is also maximum velocity of cylinder). Velocity of the cylinder will force the block to move in the opposite direction, let with velocity u. As there is no other force acting and no resistant force present in the system, hence we can apply conservation of momentum between block and cylinder.
Applying conservation of momentum,
$mv = Mu$
Putting values from question,
$1 \times v = 2 \times u$
$v = 2u$ ……………… (i)
Total energy of the system always remains conserved. As the cylinder starts from a height and attains velocity at the end, it has both potential and kinetic energy along with kinetic energy of block as it is also in motion.
Balancing the net energy of the system, when the cylinder starts and when it reaches bottom of the track. At the initial start, the body is at its highest point hence it has maximum potential energy and the cylinder is at rest hence it will not have kinetic energy. At the bottom the body has maximum velocity i.e. maximum kinetic energy and will be at ground level hence no potential energy. So, we can write energy conservation as:
Initial Potential Energy + Initial Kinetic Energy = Final Potential Energy + Final Kinetic Energy
$mg(R - r)\, + \,0 = 0 + \left( {\dfrac{1}{2}m{v^2} + \dfrac{1}{2}M{u^2}} \right)$ ………….. (ii)
Height of cylinder is considered $\left( {R - r} \right)$ because,
R is the radius of the semicircle above which the cylinder is present initially, but the centre of mass of the cylinder lies in the geometric centre of the cylinder which is at r level below R.
Putting values in equation (ii) from the question,
$1 \times 10\left( {1.1 - 0.1} \right) = \dfrac{1}{2} \times 1 \times {v^2} + \dfrac{1}{2} \times 2 \times {u^2}$
As every unit is in the S.I. system hence the radius of the cylinder is converted into S.I. unit system.
Evaluating above equation will give,
$10 = \dfrac{{{v^2}}}{2} + {u^2}$
Putting value of v from equation (i),
$10 = \dfrac{{{{\left( {2u} \right)}^2}}}{2} + {u^2}$
Evaluating above equation will yield,
$u = \sqrt {\dfrac{{10}}{3}}$
$\therefore$ When the cylinder reaches at bottom of track, the block will attain a velocity of $\sqrt {\dfrac{{10}}{3}} \,m\,{s^{ - 1}}$. So, Option (A) is correct.

Note:
Remember that the energy of the system always remains conserved in every type of situation. In presence of resistant forces also energy is conserved but with presence of energy lost or generated by those forces. Also remember to take every unit in the same unit system, either S.I. or C.G.S. and never use them together else the values yield will be quite different.