Question
Question: A block of mass \[{m_1}\] is resting on a rough horizontal plane, the coefficient of the kinetic fri...
A block of mass m1 is resting on a rough horizontal plane, the coefficient of the kinetic friction between the block and the surface is μ. If m1 is connected to another mass m2 with the help of string and pulley as shown in the figure, then the common acceleration when the system is released from the rest will be
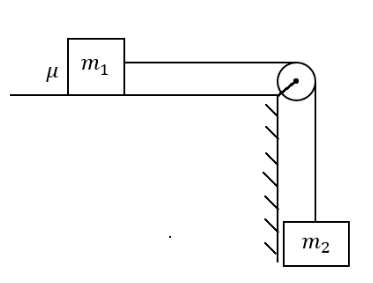
(A) m1+m2m2g
(B) m1+m2m2g
(C) m1+m2μ(m2+m1)g
(D) [m1+m2m2−μm1]g
Solution
Apply Newton’s second law of motion to both the masses and rearrange the equations you got to determine the effective acceleration of the system.
Complete step by step answer:
Draw a free body diagram to denote the forces acting on the above system as follows,
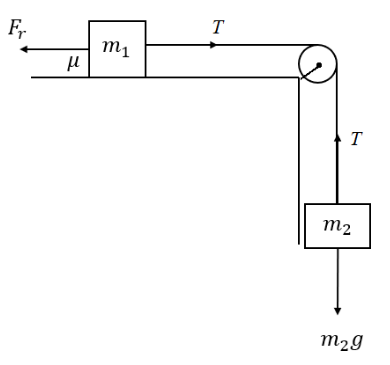
In the above free body diagram, Fr is the frictional force acting on the mass m1, T is the tension in the string, and m2g is the weight of m2.
Apply Newton’s second law of motion on the mass m1 as follows,
⇒Fnet=m1a
⇒T−Fr=m1a …… (1)
We know that the frictional force acting on the mass m1 is given by the equation,
⇒Fr=μm1g
Therefore, equation (1) becomes,
⇒T−μm1g=m1a …… (2)
Apply Newton’s second law of motion on the mass m2 as follows,
⇒T−m2g=m2(−a)
⇒T−m2g=−m2a …… (3)
Here, the negative sign of the acceleration implies that the mass is accelerated in the downward direction.
Subtract equation (2) from equation (3).
⇒T−m2g−(T−μm1g)=−m2a−m1a
⇒m2g−μm1g=(m1+m2)a
⇒∴a=(m1+m2)(m2−μm1)g
So, the correct option is (D).
Note: Always specify the direction of the forces and the direction of the acceleration of the body. In this problem, the direction of the mass m1 is towards right and hence taken positive while the direction of the acceleration of the mass m2 is downwards, hence taken as negative.
