Question

A block of mass ${m_1}$ connected with another of mass ${m_2}$ by a light spring of natural length ${l_0}$ and stiffness $k$ is kept stationary on a rough horizontal surface. The coefficient of friction between ${m_1}$ and surface is $\mu$ and the block ${m_2}$ is smooth .The block ${m_2}$ is moved with certain the block ${m_1}$ in horizontal plane Find the (a) maximum to ${m_1}$ and (b) acceleration of ${m_2}$ in part (a).

Answer 1

Hint : In order to solve this question, we are going to consider the free body diagrams of the two masses and take all the forces that are acting on them. After that we get the relations for the velocity and on solving, the maximum is found. After that the acceleration is found from the net force.
The net force for mass ${m_1}$ is
$kx = \mu N = \mu {m_1}g$
Centripetal force, ${F_C} = \dfrac{{m{v^2}}}{r}$
If ${a_2}$ is the acceleration, then force,
$F = ma$

Complete Step By Step Answer:
Let us first start by drawing the free body diagrams of both the masses
Taking the mass ${m_1}$ first

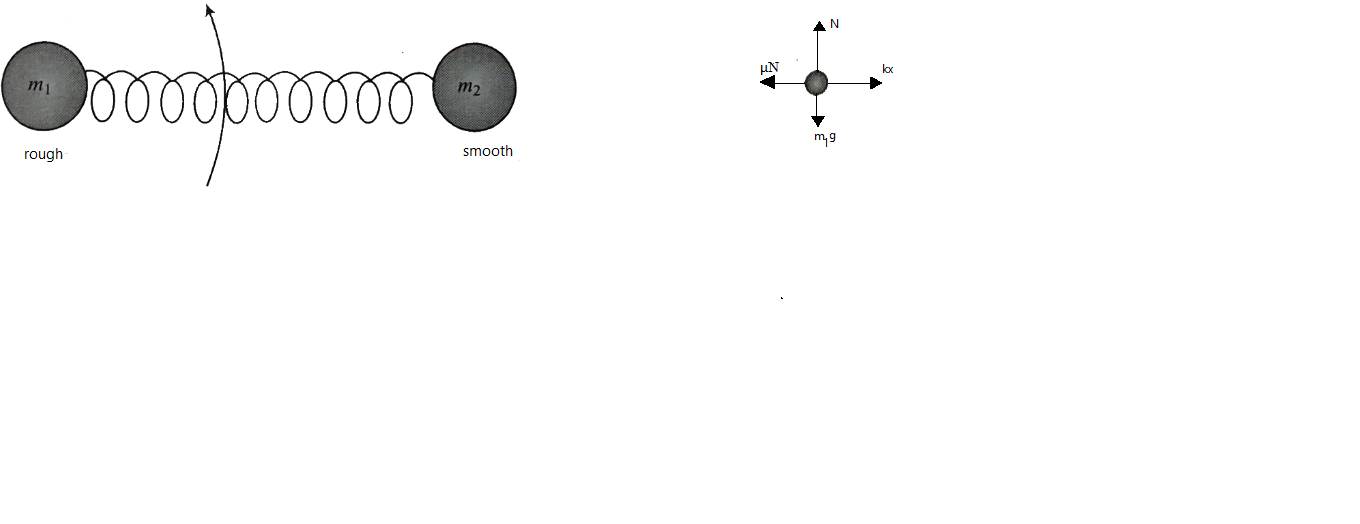
$kx = \mu N = \mu {m_1}g$
Solving for the value of $x$ ,
$x = \dfrac{{\mu {m_1}g}}{k} - - - - \left( 1 \right)$
Taking the mass ${m_2}$

Now the force $kx$ is balanced by the centripetal force, thus, considering the linear velocity to be $v$ and radial distance being ${l_0} + x$ , we get the relation as
$kx = \dfrac{{{m_2}{v^2}}}{{{l_0} + x}}$
Converting the linear velocity $v$ to angular velocity $\omega$ , we get the relation as
$kx = {m_2}{\omega ^2}\left( {{l_0} + x} \right)$
Using the value of $x$ from equation $\left( 1 \right)$ in this equation
$k\left( {\dfrac{{\mu {m_1}g}}{k}} \right) = {m_2}{\omega ^2}\left( {{l_0} + \dfrac{{\mu {m_1}g}}{k}} \right)$
Now solving for the value of the maximum velocity
{\omega ^2} = \dfrac{{\mu {m_1}g}}{{{m_2}\left( {{l_0} + \dfrac{{\mu {m_1}g}}{k}} \right)}} \\\ \omega = \sqrt {\dfrac{{\mu k{m_1}g}}{{{m_2}\left( {{l_0}k + \mu {m_1}g} \right)}}} \\\
In order to solve part (b), we need to find the acceleration on ${m_2}$
The net force on the mass ${m_2}$ is balanced by the spring force
If ${a_2}$ is the acceleration of the mass, then,
${m_2}{a_2} = kx$
Then, the acceleration becomes
${a_2} = \dfrac{{kx}}{{{m_2}}} = \dfrac{{\mu {m_1}g}}{{{m_2}}}$

Note :
As mass ${m_1}$ is lying on a rough surface, so the frictional force plays an important part, while in the case of the mass ${m_2}$ , there is no frictional force, as it lies on the smooth surface, but the only force that is acting on the mass ${m_2}$ is the spring force that depends on the extension of spring and spring constant.