Question

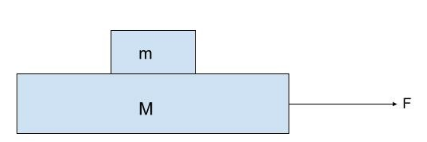
A block of mass in is placed on another block of mass M which itself is lying on a horizontal surface. The coefficient of friction between two blocks is ${\mu _1}$ and that between the block of mass M and the horizontal surface is ${\mu _2}$. What maximum horizontal force can be applied to the lower block so that the two blocks move without separation?

Answer 1

This question is based on the concept of laws of motion. It requires the knowledge of frictional forces and their properties and effects on different bodies. Frictional force is the force created when two surfaces collide and slide against one another. It is responsible for many mechanical phenomena.

Complete answer:
When the surface of one object comes into touch with the surface of another, friction is the force that resists motion. Friction reduces a machine's mechanical advantage, or, to put it another way, friction reduces the output-to-input ratio. One-quarter of an automobile's energy is spent reducing friction.

However, friction in the tyres helps the automobile to stay on the road, while friction in the clutch allows the automobile to drive. Friction is one of the most important phenomena in the physical universe, affecting everything from matches to machines to molecular structures.

In the above question,
Mass of upper block = $m$
Mass of lower block = $M$
The coefficient of friction between upper and lower block = ${\mu _1}$.
The coefficient of friction between lower block and surface = ${\mu _2}$.
The applied force should be such that frictional force acting on the upper block should be less than limiting friction (=${\mu _1}mg$)
For non-slipping condition,
Force on upper block, $f < {\mu _1}mg$ (limiting friction)
$ma = {\mu _1}mg$
$\Rightarrow a = {\mu _1}g.........(1)$
Force of friction on mass M = ${\mu _2}(M + m)g$
Let the system move with acceleration $a$. Then for whole system:
$F - {\mu _2}(M + m)g = (M + m)a..........(2)$
Solving (1) and (2), we get,
$\therefore F = (M + m)g({\mu _1} + {\mu _2})$

Maximum force applied on the lower block is $(\mu + m)g({\mu _1} + {\mu _2})$.

Note: The reaction between two solid bodies in contact when they are in motion (kinetic friction) and when they are not (dry friction) is described by dry friction (static friction). The normal force exerted between the solid bodies is proportional to both static and kinetic friction. Different coefficients of friction are used to represent the interaction of different substances.