Question

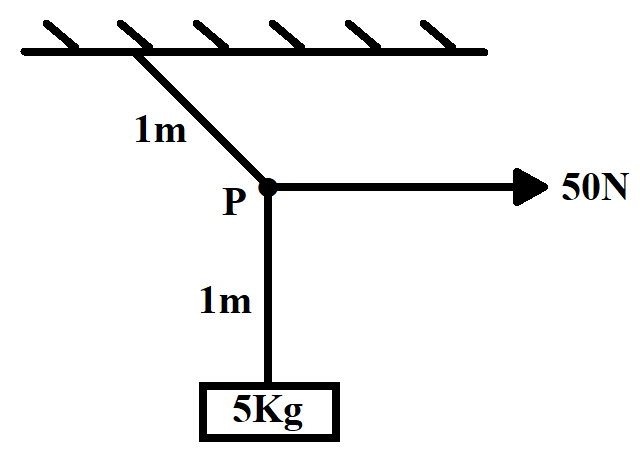
A block of mass $5Kg$ is suspended by a massless rope of length $2m$ from the ceiling. A force of $50N$ is applied in the horizontal direction at the midpoint P of the rope, as shown in the figure.
The angle made by the rope with the vertical in equilibrium is (Take $g=10m{{s}^{-2}}$)

& \text{A}\text{. }{{30}^{\circ }} \\\ & \text{B}\text{. }{{40}^{\circ }} \\\ & \text{C}\text{. }{{60}^{\circ }} \\\ & \text{D}\text{. }{{45}^{\circ }} \\\ \end{aligned}$$

Answer 1

For the system to be in equilibrium, both the block and the point P should be in equilibrium. We will draw the free body diagram for both of them and balance the forces acting on them in horizontal direction and vertical direction. This will result in the determination of the angle made by the rope with the vertical in equilibrium.

Complete step by step answer:
Equilibrium is described as the state of a system in which all the forces acting upon it are balanced in all the directions. In such cases, the net force on the system is zero Newton. Knowing the forces acting upon the system, trigonometric functions can be utilized to determine the horizontal and the vertical components of each force.
We are given that a block is suspended with the help of a massless rope and a force is applied on at the midpoint of the rope. We need to calculate the angle which the rope makes with the vertical in equilibrium state.

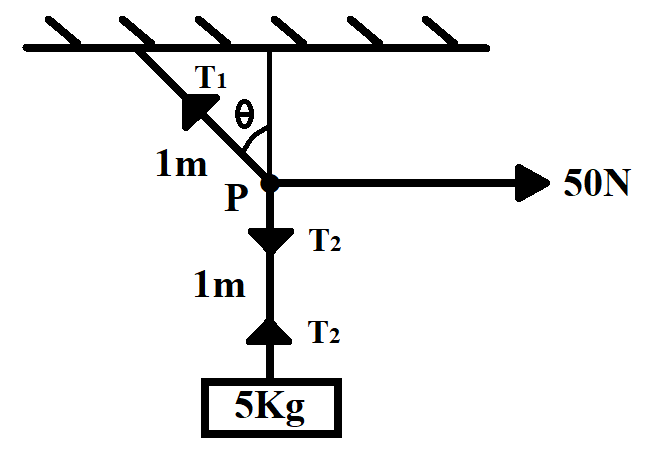
Let $\theta$ be the angle made by the rope with the vertical in equilibrium.
Let ${{T}_{1}}$ and ${{T}_{2}}$ be the tension in the ropes as shown in the figure.
The free body diagram of $5Kg$ block is shown below.

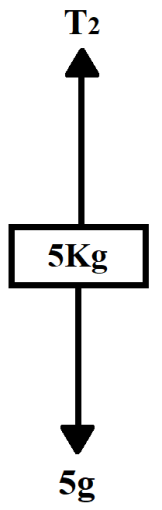
In equilibrium position,
${{T}_{2}}=5g$
Put $g=10m{{s}^{-2}}$
We get,
${{T}_{2}}=5\times 10=50N$
The free body diagram of P is shown below.

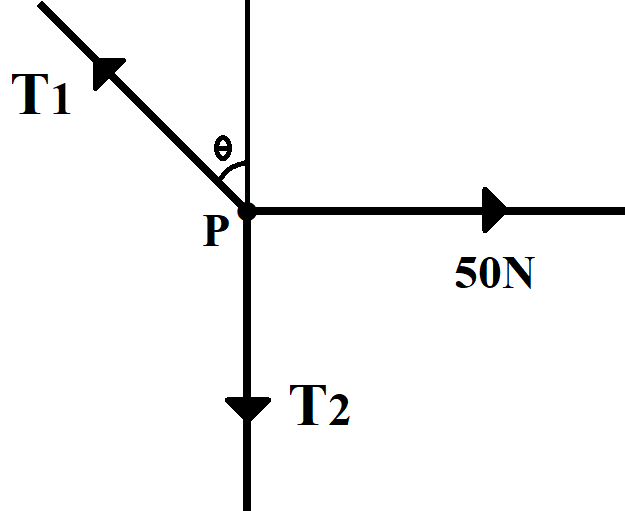
In equilibrium position,
${{T}_{1}}\sin \theta =50N$
(Let’s say equation 1)
And,
${{T}_{1}}\cos \theta ={{T}_{2}}=50N$
(Let’s say equation 2)
Dividing equation 1 and equation 2,
$\begin{aligned} & \dfrac{{{T}_{1}}\sin \theta }{{{T}_{1}}\cos \theta }=\dfrac{50}{50} \\\ & \tan \theta =1 \\\ & \theta ={{45}^{\circ }} \\\ \end{aligned}$
The angle made by the rope with the vertical in equilibrium is ${{45}^{\circ }}$
Hence, the correct option is D.

Note:
To attain the equilibrium position, all the forces acting on a system should be zero in all the directions.
The massless rope signifies that the downward force acting on the block is only due to the weight of the block, and has nothing to do with the weight of the rope.