Question

A block of mass $50kg$ is pulled up a slope with constant speed by applying an external force of $20kgf$ parallel to the slope. The block moves through a distance of $4m$ along the slope.
What is the work done by the external applied force?
What is the energy stored when it reaches the vertical height of $3m$ ($g = 10\dfrac{m}{{{s^2}}}$)

Answer 1

The block is under the effect of two forces. The constant force moves it up the slope and its weight increases its potential energy. The work done is the product of force and displacement and potential energy is the product of weight and height of the body. Substituting corresponding values, we can calculate both work and potential of the body.

Formula used:

$$W = Fx \\\ P = F'h \\\$$

Complete step by step solution:

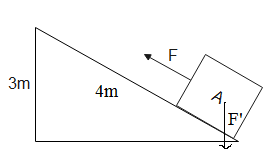
In the given figure, $F$ is the constant force while $F'$ is the weight of the block.
The work done is given by-
$W = Fx$
Here, $W$ is the work done
$F$ is the force acting on the body
$x$ is the displacement travelled by the body

$$F = 20kgf = 20 \times 10N = 200N\left( {\therefore 1kgf = 10N} \right) \\\ x = 4m \\\$$

Substituting given values in the above equation, we get,
$W = 200 \times 4 = 800J$
The work done on the block by the constant force is $800J$
The potential energy (P) of a body is given by-
$P = F'h$
$F'$is the weight of the body
$h$is the height
$F' = 50kg = 50 \times 10 = 500N,h = 3m$Substituting given values in the above equation, we get,
$P = 500 \times 3 = 1500J$

Note: The potential energy and work done have the same units. The potential of a body due to gravity is always negative. Work done is a scalar quantity. Both forces acting on the body are constant; hence the acceleration of the body will also be constant. Energy is the ability of a body to do work.