Question

A block of mass $5\;kg$ is placed on a rough horizontal surface and a pushing force of $20\;N$ is applied to the block as shown in the figure. If the coefficient of static friction between the block and the surface is $0.2$, then the frictional force is $\left( {g = 10\;m/{s^2}} \right)$.

(1) 3.2 N
(2) 6.4 N
(3) 12.8 N
(4) 16 N

Answer 1

: For the frictional force's determination, we have to draw the free body diagram because the free body diagram gives us information about the types of forces acting on the block. After this, use the expression ${f_r} = \mu N$ for the determination of frictional force.

Complete step by step solution:
It is given to us that the mass of the block is $5\;kg$, coefficient of friction is $0.2$, acceleration due to gravity is $10\;m/{s^2}$ and magnitude of the applied pushing force is $20\;N$, so we will use this information for the determination of frictional force.

Draw the block's free-body diagram and take the applied force's horizontal and vertical components for the calculation for frictional force.

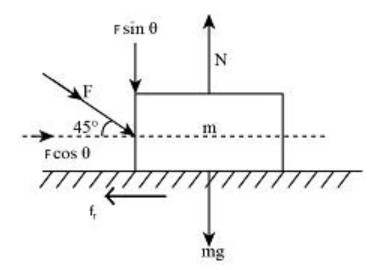
From a free-body diagram, it is very clear that the normal force is acting upward. So we will resolve the force in the force in the vertical direction.

Therefore, we get

$N = mg + F\sin \theta$

Substitute the values in the above equation.

$N = mg + F\sin \theta$

Here, $m$ is the mass of the block, $g$ is the acceleration due to gravity, $F$ is the applied pushing force and $\theta$ is the angle at which the pushing force is applied.

Substitute the values in the above equation.

$\begin{array}{l} N = \left( {5\;kg \times 10\;m/{s^2}} \right) + \left( {20\;N \times \sin 45^\circ } \right)\\\ N = 50\;N + 14.14\;N\\\ N = 64.14\;N \end{array}$

We know that the frictional force depends on the coefficient of friction and magnitude of normal force, so write the expression of frictional force as,

${f_r} = \mu N$

Here, $\mu$ is the coefficient of friction.

Now we will substitute the values of normal force and coefficient of static friction in the above equation.

Therefore, we get

$\begin{array}{l} {f_r} = 0.2 \times 64.14\;N\\\ {f_r} = 12.8\;N \end{array}$

Therefore, the magnitude of the frictional force is $12.8\;N$, and option (3) is correct.

Note: Remember that normal force always acts opposite the surface and use this information while you draw the free body diagram. Also, remember that the frictional force directly depends on the normal force and friction coefficient to obtain its magnitude.