Question

A block of mass $4kg$ slides down an inclined surface of inclination ${{30}^{{}^\circ }}$ with the horizontal. A force of 4N is applied on the block. If the coefficient of friction is 0.11 then, how far will the block move in the first two seconds after starting from rest?

Answer 1

When an object is placed at an inclined surface, it experiences some force downward due to the component of gravitational force acting on it. The acceleration of the block can be determined using equations of motion and the distance travelled can be determined using the formula for distance due to constant acceleration.

Complete step by step answer:
When an object is placed at an inclined surface, it experiences some force downward due to the component of gravitational force acting on it.
Firstly, we resolve the components acceleration in direction of motion and perpendicular to direction of motion.

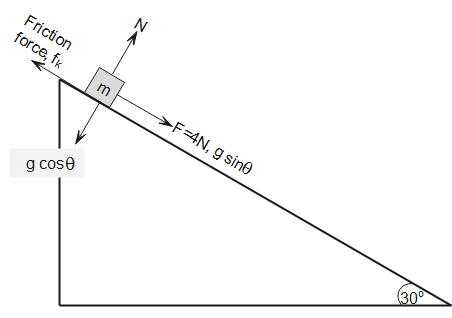
Equation of motion along the direction of motion can be written as
${{F}_{b}}+mg\sin \theta ={{f}_{k}}$
In direction perpendicular to direction of motion
$N=mg\cos \theta$
Along the direction of motion net force when object accelerates with acceleration $a'$ is
${{F}_{net}}=ma$
This implies that,
${{F}_{b}}+mg\sin \theta -{{f}_{k}}=ma$
Where kinetic friction force ${{f}_{k}}=\mu N$
$\mu$ is the coefficient of kinetic friction.
$\Rightarrow {{f}_{k}}=\mu mg\cos \theta$
Therefore, we get
$a=\dfrac{{{F}_{b}}}{m}+g(\sin \theta -\mu \cos \theta )$
Substituting the values from given data, we have
$a=\dfrac{4N}{4kg}+10m/{{s}^{2}}\left( \sin {{30}^{{}^\circ }}-0.11\cos {{30}^{{}^\circ }} \right)$
Solving this, we get
$a=5.055m/{{s}^{2}}$
For constant acceleration, the distance covered by a body is given by $s=ut+\dfrac{1}{2}a{{t}^{2}}$
As initially block starts from rest the distance travelled by it in first two seconds is
$s=0+\dfrac{1}{2}\times 5.055\times {{(2)}^{2}}=10.11m$

Note: Friction is a force that comes into play when two surfaces are in contact with each other when some force tries to move one body. Friction always opposes the motion of the body thus slowing it down. Normal reaction force is the force exerted by a surface perpendicular to the surface of the object which is in contact with it.