Question

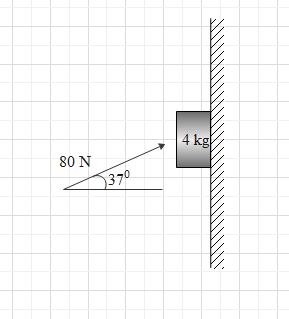
A block of mass 4kg is pressed against the wall by a force of $80\,N$ as shown in figure. Determine the value of friction force and block’s acceleration (take ${\mu _s} = 0.2$ , ${\mu _k} = 0.15$).

A. $8\,N$ , $0\,m/{s^2}$
B. $32\,N$ , $6\,m/{s^2}$
C. $8\,N$ , $6\,m/{s^2}$
D. $32\,N$ , $2\,m/{s^2}$

Answer 1

By analysing all the forces acting on the block. We can find that the sine component of force is balanced by the weight and frictional force. Cosine component of force is balanced by the normal reaction force. From this we can find the frictional force. If the value of frictional force is less than the limiting friction there will be no acceleration of the block.

Complete step by step answer:
It is given that a block of mass $4kg$ is pressed against the wall by a force of $80N$
Mass, $m = 4\,kg$
Force, $F = 80\,N$
We need to find the value of force due to friction and the acceleration of the block.
Consider the diagram given below showing all the forces acting on the block.

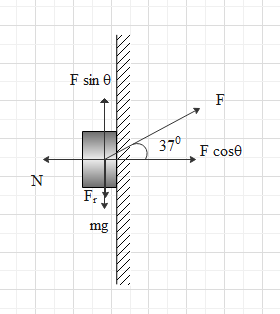
The component of applied force in the horizontal direction is $F\cos \theta$ and component of force in the vertical direction is $F\sin \theta$
$F\cos \theta = F\cos {37^ \circ } = 80 \times 0.8$
$\Rightarrow F\cos \theta = 64\,N$
$F\cos \theta = F\sin {37^ \circ } = 80 \times 0.6$
$\Rightarrow F\sin \theta = 48\,N$
We know weight is the product of mass, m and acceleration due to gravity g. since g is not given let us take its value as $10\,m/{s^2}$.
Weight, $W = mg = 4 \times \,10 = 40\,N$
The cosine component of force is balanced by the normal reaction of the wall.
Thus
$N = F\cos \theta = 64N$
Now we know that the maximum value of friction called the limiting friction is the product of the coefficient of static friction and normal reaction.
${F_{\lim }} = {\mu _s}N$
Where ${\mu _s}$is the slate friction.
Value of ${\mu _s}$ is given as $0 \cdot 2$ .
On substituting the values, we get
$\Rightarrow {F_{\lim }} = 0 \cdot 2 \times 64 = 12 \cdot 8N$
The motion will occur only if we overcome this maximum value of friction.
We can see that the vertical component of force is balanced by the weight and frictional force
$\Rightarrow F\sin \theta = mg + {F_r}$
$\Rightarrow F\sin \theta - mg = {F_r}$
$\Rightarrow 48 - 40 = {F_r}$
$\therefore {F_r} = 8N$
This value is less than the value of limiting friction. So there will not be any motion.
So, the acceleration of the block is zero.
$\therefore a = 0$

$\therefore$ The value of friction force is 8N. And the block’s acceleration is zero. Hence, the correct answer is option A.

Note:
Remember that the limiting friction is the maximum value of friction. The motion will occur only if we overcome this value of friction. The limiting friction is calculated as
${F_{\max }} = {\mu _s} \cdot N$
Where, ${\mu _s}$ is the coefficient of static friction and $N$ is the normal reaction force.